


suivant: La 2B-consistance
monter: Méthodes de filtrage local
précédent: Méthodes de filtrage local
Table des matières
Nous allons dans cette section, donner les définitions de bases de l'arithmétique des intervalles [17],
nécessaire à la compréhension des techniques de filtrage locale dans les domaines continus.
Un intervalle ![$ [a,b]$](img97.png) avec
avec 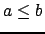 est l''ensemble des valeurs réelles comprises entre
est l''ensemble des valeurs réelles comprises entre 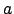 et
et 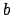 .
L'arithmétique des intervalles est une extension de l'arithmétique sur les réels et définit les opérations
.
L'arithmétique des intervalles est une extension de l'arithmétique sur les réels et définit les opérations
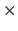 ,
, 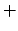 ,
, 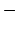 , et
, et 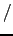 de la manière suivante :
La commutativité et l'associativité est respectée pour l'addition et la multiplication mais pas la distributivité dans le cas
général.
On peut étendre cet arithmétique de base aux fonctions mathématiques de base(exponentielle, logarithme, puissance
de la manière suivante :
La commutativité et l'associativité est respectée pour l'addition et la multiplication mais pas la distributivité dans le cas
général.
On peut étendre cet arithmétique de base aux fonctions mathématiques de base(exponentielle, logarithme, puissance 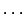 ),
mais le résultat de l'application d'une fonction à un intervalle n'est pas toujours un intervalle.
C'est le cas lorsque la fonction est continue et monotone sur l'intervalle.
Lorsque la fonction n'est pas monotone sur un intervalle, il faut le décomposer en domaines sur lesquels la fonction
est monotone.
La règle de base de l'arithmétique des intervalles est que si
),
mais le résultat de l'application d'une fonction à un intervalle n'est pas toujours un intervalle.
C'est le cas lorsque la fonction est continue et monotone sur l'intervalle.
Lorsque la fonction n'est pas monotone sur un intervalle, il faut le décomposer en domaines sur lesquels la fonction
est monotone.
La règle de base de l'arithmétique des intervalles est que si
![$ x \in [a,b]$](img114.png) alors
alors
![$ f(x) \in F([a,b]$](img115.png) ,
avec
,
avec 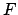 extension de
extension de 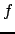 aux intervalles.
aux intervalles.
Fonction de projection :
Les techniques de consistance locale utilisent une fonction de projection d'une contrainte pour mettre à
jour le domaine d'une variable. Pour une contrainte 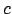 mettant en jeu les variables
mettant en jeu les variables
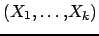 ,
il s'agit d'exprimer la variable
,
il s'agit d'exprimer la variable 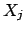 en une fonction
en une fonction 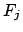 des autres variables.
La valeur de retour est l'intersection entre le domaine de
des autres variables.
La valeur de retour est l'intersection entre le domaine de 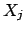 et
l'application de
et
l'application de 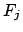 aux domaines des autres variables.
aux domaines des autres variables.



suivant: La 2B-consistance
monter: Méthodes de filtrage local
précédent: Méthodes de filtrage local
Table des matières
Heikel Batnini
2002-10-22