Motivations

On peut définir notre problème de la manière suivante : Soient $n$ points dans un espace euclidien $\mathbb{R}^p$, fixés ou contraints à appartenir à un domaine fermé de $\mathbb{R}^p$. Étant données les distances, exactes ou approximatives, entre $m$ couples de points parmi les $\frac{n(n-1)}{2}$ vecteurs possibles, on cherche à déterminer l'existence ou non de combinaisons de points respectant les contraintes de distance et de localisation imposées. Si c'est le cas, on cherche alors à réduire le volume des domaines de variations des points, c'est à dire à éliminer un maximum de valeurs inconsistantes pour lesquelles toute combinaison de points dans laquelle ils figurent ne peut être solution du système.
Souvent plongé à l'intérieur d'un système de contraintes, le problème de satisfaction de contraintes de distance se retrouve dans de nombreux domaines d'application. On peut en citer deux parmi d'autres :

• En biologie moléculaire : Lorsqu'on veut faire de la conformation de molécules, on mesure expérimentalement les distances interatomiques ainsi que les angles entre les liaisons. On engendre alors un ensemble de contraintes géomètriques, auquel on ajoute d'autres types de contraintes comme des contraintes liées à la polarisation des atomes ou aux angles de torsion entre les liaisons. La résolution de ce système permet d'une part de modéliser la molécule étudiée et d'en faire un rendu graphique, et d'autre part de générer les conformères de cette molécule, ce qui facilite le travail de recherche des chimistes, notemment lorsqu'il s'agit de trouver de nouveaux médicaments.
• En théorie des mécanismes et plus généralement en CAO : Lors de la conception optimale d'un robot, on souhaite que tout point de son espace de travail soit accessible, le plus rapidement et en consommant le moins d'énergie possible. On résout alors un système de contraintes de distances dans lequel les points sont les articulations du robot, les domaines des points sont bornés par l'espace de travail et les distances sont les longueurs de ses membres.

Nous allons tout d'abord nous attacher à définir une instance de notre problème de manière plus formelle. Puis nous étudierons les outils offerts par la programmation par contraintes pour résoudre ce problème. Nous définirons la notion de contrainte globale, illustrée par des exemples dans les domaines finis. Noue étudierons également les limites des méthodes de consistances locales pour les contraintes de distances. Ensuite nous verrons comment on peut, dans certains cas, améliorer la qualité des résultats des méthodes usuelles de filtrage local, par un algorithme de fermeture d'une instance avec filtrage à la volée. Cet algorithme permet de calculer les domaines des distances manquantes et de réduire les domaines des distances données, de manière à respecter les inégalités triangulaires. On obtient ainsi un graphe de contraintes complet, avec une propriété intéressante : Toute instanciation de trois distances dans leurs domaines permet toujours de construire le triangle ainsi formé. L'idée que nous avons eu est d'ajouter à cet algorithme de fermeture, une procédure de filtrage des domaines des coordonnées des points, afin d'étendre d'une certaine manière cette propriété. Le principe de cette technique [2] est de calculer un filtrage global des domaines en résolvant des sous-problèmes à la volée. Nous avons donc développé deux stratégies de filtrage à la volée :

• Un filtrage simple des domaines des coordonnées des points mis en jeu par une seule contrainte.
• Une consistance locale sur des sous-problèmes triangulaires dans lesquels on a ajouté des contraintes redondantes, pour permettre un meilleur filtrage.

Ces deux méthodes nous donnent un pré-filtrage des domaines, permettant ensuite aux méthodes de consistance locale d'être plus efficaces et plus précises dans certains cas.

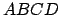
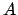
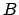
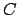
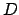
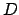
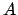
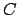
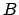
Exemple 1.1 (Un exemple simple : Un quadrilatère)   Dans un quadrilatère $ABCD$, on connaît les longueurs de tous ses côtés ainsi que les coordonnées fixées de deux sommets $A$ et $B$. Nos deux inconnues sont donc les points $C$ et $D$. 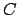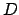Sachant que $D$ appartient au cercle centré en $A$ et de rayon 3, et que $C$ appartient au cercle de centre $B$ et de rayon 2, quelles sont les coordonnées de $C$ et $D$ qui valident la distance $CD$. 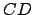Prenons par exemple les valeurs suivantes :

$A(0,0)$, $B(8,0)$, $C(x_C,y_C)$, $D(x_D,y_D)$
$AB=8$, $AD=3$, $BC=2$, $CD=4$
$D_{x_C}=[6,10]$, $D_{y_C}=[-2,2]$
$D_{x_D}=[-3,3]$, $D_{y_D}=[-3,3]$

Ce qui nous conduit à poser le système sous-contraint :

$C_1$:	${(x_C - 8)}^2 + {y_C}^2$	$=$	$4$
$C_2$:	${(x_D - x_C)}^2 + {(y_D - y_C)}^2$	$=$	$16$
$C_3$:	${x_D}^2 + {y_D}^2$	$=$	$9$

Ce système possède une infinité de solutions (voir la figure 2 à la page ).