Next: Conclusion Up: Real-time Collision Detection for Previous: Taking the motion of

Results

**Figure 9:** Collision detection between a triangular mesh modeling a human liver and a static position of a tool (which is visualized as a segment).
$\begin{figure} \begin{center}\leavevmode % \epsfbox{Figures/static.2.eps} \end{center} \end{figure}$

**Figure 10:** Dynamic collision detection, where the tool motion during a time interval is taken into account (this volume covered by the tool is visualized as a single triangle).
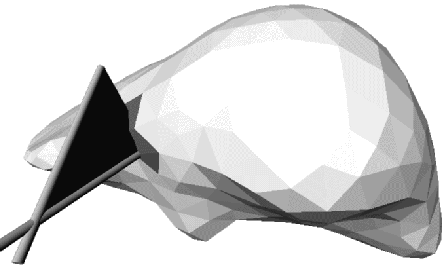$\begin{figure} \begin{center}\leavevmode % \epsfbox{Figures/dynamic.2.eps} \end{center} \end{figure}$

**Figure 11:** Collision detection times
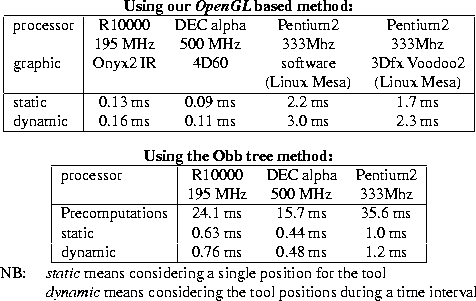$\begin{figure}{% \begin{center} \textbf{Using our \emph{OpenGL\,}based method:}... ...ool positions during a time interval\\ \end{tabular}\end{center}} \end{figure}$

**Figure 12:** Acceleration factor provided by our method w.r.t. *RAPID*
$\begin{figure}{% \begin{center} \begin{tabular}{\vert r\vert c\vert c\vert c\ve... ...s igonring RAPID's precomputation time. \end{tabular}\end{center}} \end{figure}$

We have done a series of cross-tests to bench our collision methods:

using our liver geometry (1224 triangles) or a simple tetrahedron (4 triangles),
testing either static collisions with the tool at a time step (`static') or collision with the volume covered by the tool during a time interval (`dynamic'), as depicted in Figures 9 and 10,
testing dynamic collision with different numbers of colliding faces (between 5 and 25 for the liver, between 0 and 3 for the tetrahedron).
comparing our method with the reference software package RAPID² implementing Obb trees [5],
running on various hardwares and graphic accelerators.

Figure 11 sums up the comparisons of computational times between our method and the RAPID software on various platforms (each given time is a mean value between ten trials of different collision configurations). Since the same compiler (gcc/egcs) was used on all platforms for compatibility reasons, the results cannot be used for a direct comparison between platforms (gcc uses to produce inefficient code on SGI). The meaningful comparison is the ratio between the two methods depending on the graphics and computational performances of the platform³.

The Obb tree method used in RAPID needs precomputing the hierarchical data structure. In our application where the liver deforms over time, RAPID's data-structure would have to be updated at each time step. Since there is no method for doing so to the authors knowledge, we compared our method with the use of RAPID where pre-computations are redone at each time step. Our method then brings an acceleration factor from 150 on high-end hardwares to 12 with a software implementation of OpenGL(however,Obb trees would probably give better results if an efficient update algorithm taking advantage of temporal coherence was developed). To be fair, we also computed the acceleration factor without taking RAPID's pre-computation into account. Even in this case which is only applicable to rigid objects, our method nearly brings an acceleration factor of five for each collision detection on high-end hardware. All these results are summarized in Figure 12.

Next: Conclusion Up: Real-time Collision Detection for Previous: Taking the motion of

Jean-Christophe Lombardo
1999-05-17