Next: Results Up: Real-time Collision Detection for Previous: Static Collision Detection

Taking the motion of the tool into account

The simple solution presented in the previous section tests the collision between a static position of the tool and the organ at a given time step. This suffers from the classical flaws of time discretization: if the user hands move quickly, the tool may deeply penetrate inside the organ before being repulsed. It may even cross a thin part of the organ without any collision being detected.

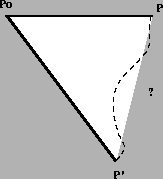
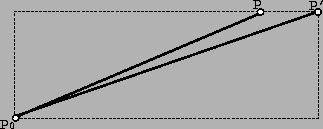
**Figure 3:** Tool movement between two simulation steps.
$\begin{figure} \begin{center}\leavevmode \epsfysize=4cm\epsfbox{Figures/triangle.eps} \end{center} \end{figure}$

**Figure 4:** Volume covered by the tool during a time interval.
$\begin{figure} \begin{center}\leavevmode \epsfysize=4cm\epsfbox{Figures/area.eps} \end{center} \end{figure}$

In order to avoid these classical problems, we present an extension which takes into account the volume covered by the tool during a time step (we still neglect the dynamic deformations of the organ during this time period). In our model, the tool goes through the patient's abdominal wall at the fixed point P₀, and is able to slide through this point, so its length varies over time. We assume that the active extremity of the tool follows a straight line trajectory from P to P'. The area covered by the axis of the tool is thus the triangle P₀,P,P' (see Figure 3). 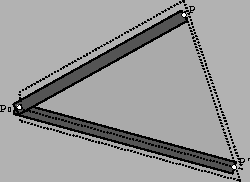Since the tool may be seen as a cylinder of radius s, the volume covered by the tool during the time-interval is obtained by enlarging and thickening the triangle by the distance s. It is thus an hexahedron, as shown in Figure 4. As in the previous section, our aim is to model this volume using OpenGLcameras and clipping planes.

Figure 4: Volume covered by the tool during a time interval.
$\begin{figure} \begin{center}\leavevmode \epsfysize=4cm\epsfbox{Figures/area.eps} \end{center} \end{figure}$

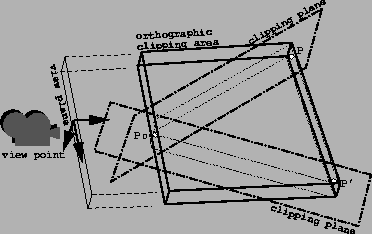
The simplest way to do this consists in using an orthographic projection, which parallelepipedic viewing volume corresponds to the bounding box of the hexahedron (see Figure 5): bottom and top, near and far correspond to the hexahedron; two extra clipping planes are used to model the sides P₀P and P₀P'.

Figure 5: Naive approach using an orthographic camera.
$\begin{figure} \begin{center}\leavevmode \epsfysize=5.4cm\epsfbox{Figures/ortho.eps} \end{center} \end{figure}$

**Figure 5:** Naive approach using an orthographic camera.
$\begin{figure} \begin{center}\leavevmode \epsfysize=5.4cm\epsfbox{Figures/ortho.eps} \end{center} \end{figure}$

**Figure 6:** Configuration where the viewing volume is much too large before the addition of the two extra clipping planes.
$\begin{figure} \begin{center}\leavevmode \epsfysize=3cm\epsfbox{Figures/bad.eps} \end{center} \end{figure}$

However, this naive construction has some flaws. For instance, the orthographic viewing volume will be excessively large when PP' is far from orthogonal to P₀P (see Figure 6). The consequence is that a lot of faces will be accepted during the clipping with the frustum, and rejected later during clipping with the user-defined clipping-planes. This increases the cost, since the latter is more computationally intensive than clipping with the canonical viewing volume.

Figure 6: Configuration where the viewing volume is much too large before the addition of the two extra clipping planes.
$\begin{figure} \begin{center}\leavevmode \epsfysize=3cm\epsfbox{Figures/bad.eps} \end{center} \end{figure}$

Thus, we construct the test-volume using OpenGLin a more complex way, in order to use intermediary volumes that are as small as possible. Our construction is based on a perspective viewing volume whose cone follows the segments P₀P and P₀P', as shown in Figure 7. This is done by setting the camera axes to PP' for the x axis, 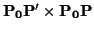$\mathbf{P_0P' \times P_0P}$ for the y axis, and $\mathbf{PP' \times (P_0P' \times P_0P)}$ for the z axis.

Figure 7: (x,z) plane of the perspective camera
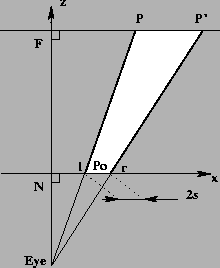$\begin{figure} \begin{center}\leavevmode \epsfysize=6cm\epsfbox{Figures/planX.eps} \end{center} \end{figure}$

**Figure 7:** (x,z) plane of the perspective camera
$\begin{figure} \begin{center}\leavevmode \epsfysize=6cm\epsfbox{Figures/planX.eps} \end{center} \end{figure}$

**Figure 8:** Reducing the viewing volume with clip planes
$\begin{figure} \begin{center}\leavevmode \epsfysize=3.5cm\epsfbox{Figures/clip.eps} \end{center} \end{figure}$

As previously, the triangle is enlarged on each side by the tool section s. We set the (top,bottom) interval in the near clipping plane to 2s. Since the camera is a perspective camera, we have to add two extra clipping planes in order to limit the vertical extent of the volume to 2s everywhere (see Figure 8).

Figure 8: Reducing the viewing volume with clip planes
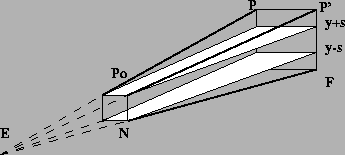$\begin{figure} \begin{center}\leavevmode \epsfysize=3.5cm\epsfbox{Figures/clip.eps} \end{center} \end{figure}$

To set the camera to this configuration, the eye position E must be computed from the points P₀, P, P'. Let u be:

$\begin{displaymath}\mathbf{u} = \frac{\mathbf{PP'}}{\Vert\mathbf{PP'}\Vert} \end{displaymath}$

We use it to set the left and right limits of the viewing volume in the near and far clipping planes:

P_0l = P₀ - s u

P_0r = P₀ + s u

P_l = P - s u

P'_r = P' + s u

From Thales theorem we get:

$\begin{displaymath}\frac{\Vert\mathbf{EP_{0l}}\Vert}{\Vert\mathbf{EP_l}\Vert} =... ...{\Vert\mathbf{P_{0l}P_{0r}}\Vert}{\Vert\mathbf{P_lP'_r}\Vert} \end{displaymath}$

This yields:

$\begin{displaymath}\mathbf{E} = \mathbf{P_{0l}} - \frac{\Vert\mathbf{P_{0l}P_{0r... ..._r}\Vert - \Vert\mathbf{P_{0l}P_{0r}}\Vert} \mathbf{P_{0l}P_l} \end{displaymath}$

Thus we set the OpenGLperspective camera parameters to:

$\begin{displaymath}L= \mathbf{EP_{0l}} \cdot \mathbf{u}\end{displaymath}$

R= L + 2s

$\begin{displaymath}N= \Vert\mathbf{EP_{0l}} - L \mathbf{u}\Vert\end{displaymath}$

$\begin{displaymath}F= \Vert\mathbf{EP_l} - (\mathbf{EP_l} \cdot \mathbf{u})\mathbf{u}\Vert\end{displaymath}$

T= +s

B= -s

We finally add the two extra clipping planes y=-s and y=s depicted in Figure 8. This leads to the following pseudo-code, where fixed is P₀, oldPos is P, and newPos is P':
glMatrixMode (GL_PROJECTION); glLoadIdentity (); u = (newPos - oldPos) /norm(newPos-oldPos); P0l = fixed - s*u; P0r = fixed + s*u; Pl = oldPos - s*u; Pr = newPos + s*u; E = P0l; E -= norm(P0l - P0r) /(norm(Pl - Pr) - 2*s) * (Pl - P0l); L = dot(P0l-E, u); R = L+2*s; B = -s; T = s; near = norm (P0l-E - L*u); far = norm (Pl-E - dot(Pl-E,u)*u); // define the projection glFrustum(L, R, B, T, near, far); glMatrixMode (GL_MODELVIEW); glLoadIdentity (); // clipping planes have to be placed in // MODELVIEW matrix, but we define them // if camera referential, so define them // BEFORE gluLookAt() GLdouble plan1[4] = {0,1,0,s}; GLdouble plan2[4] = {0,-1,0,s}; glClipPlane(GL_CLIP_PLANE0, plan1); glClipPlane(GL_CLIP_PLANE1, plan2); up = cross(E-Pr, E-Pl); F = (Pl - dot(Pl-E, u)*u); // move the camera to set eye at E // and looking at F, with up set up[] gluLookAt(E[0], E[1], E[2], F[0], F[1], F[2], up[0], up[1], up[2]); // activate the clipping planes glEnable(GL_CLIP_PLANE0); glEnable(GL_CLIP_PLANE1); // redraw the scene with some glNames // pushed redraw(NULL); glDisable(GL_CLIP_PLANE0); glDisable(GL_CLIP_PLANE1);

Next: Results Up: Real-time Collision Detection for Previous: Static Collision Detection
Jean-Christophe Lombardo
1999-05-17