



Next: An alternative: the single
Up: Mathematical background
Previous: Principle
Contents
Managing the bisection and ordering
The second problem is solved in the following way: assume that at some
step of the algorithm the bisection process leads to the creation of
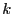
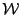 such that
such that 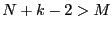 . As we have previously considered the
. As we have previously considered the
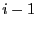 elements of
elements of 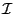 we may use them as storage space. This
means that we will store
we may use them as storage space. This
means that we will store
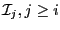 at
at
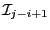 thereby freeing
thereby freeing 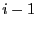 elements. In that case the procedure will fail
only if
elements. In that case the procedure will fail
only if 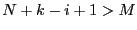 .
.
Now we have to manage the ordering of the 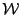 . We have defined
two types of order for a given set of boxes
. We have defined
two types of order for a given set of boxes 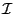 :
:
- maximum equation ordering: the box are ordered
along the value of
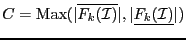 for
all
for
all 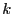 in [1,
in [1, ]. The first box will have the lowest
]. The first box will have the lowest 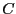 .
.
- maximum middle-point equation ordering: let
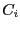 be the
vector whose components are the middle points of the intervals
be the
vector whose components are the middle points of the intervals 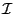 .
The box are ordered
along the value of
.
The box are ordered
along the value of
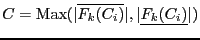 for
all
for
all 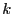 in [1,
in [1, ]. The first box will have the lowest
]. The first box will have the lowest 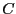 .
.
When adding the 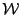 we will substitute the
we will substitute the 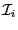 by the
by the
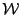 having the lowest
having the lowest 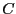 while the others
while the others 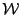 will be
added to the list
will be
added to the list 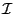 by increasing order of
by increasing order of 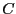 .
The purpose of these ordering is to try to consider first the
box
having the highest probability of containing a solution.
This ordering may have an importance in the determination of the
solution intervals (see for example section 2.3.5.2).
.
The purpose of these ordering is to try to consider first the
box
having the highest probability of containing a solution.
This ordering may have an importance in the determination of the
solution intervals (see for example section 2.3.5.2).
This method of managing the bisection is called the
Direct Storage mode and is the default mode in ALIAS. But
there is another mode, called the Reverse Storage
mode.
In
this mode we still substitute the 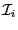 by the
by the
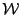 having the lowest
having the lowest 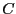 but instead of adding the remaining
but instead of adding the remaining 
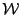 at the end of the list
at the end of the list 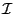 we shift by
we shift by  the
boxes in the list, thereby freeing the storage of
the
boxes in the list, thereby freeing the storage of
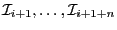 which is used to store the remaining
which is used to store the remaining 
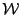 . In other words we may consider the solving procedure as
finding a leaves in a tree which are solutions of the problem: in the
Direct Storage mode we may jump during the bisection from one
branch of the tree to another while in the Reverse storage mode
we examine all the leaves issued from a branch of
the tree before examining the other branches of the tree. If we are
looking for all the solutions the storage mode has no influence on the
total number of boxes that will be examined. But the Reverse
Storage mode may have two advantages:
. In other words we may consider the solving procedure as
finding a leaves in a tree which are solutions of the problem: in the
Direct Storage mode we may jump during the bisection from one
branch of the tree to another while in the Reverse storage mode
we examine all the leaves issued from a branch of
the tree before examining the other branches of the tree. If we are
looking for all the solutions the storage mode has no influence on the
total number of boxes that will be examined. But the Reverse
Storage mode may have two advantages:
- if we are looking for only one solution it may enable to find it
more rapidly (but that is not compulsory, see section 2.3.5.4),
- as we are following one branch at a time we will consider very
rapidly small box that either will lead to a solution or
will be discarded thereby enabling to free some storage space. Hence
the storage space available in the reverse mode will be in general
higher than in the direct mode: a practical consequence is that a
problem may not be solved with the direct mode due to problem in the
storage while with the same amount of storage solutions will be
obtained in the reverse mode.
To switch the storage mode see section 2.3.4.5 .We may also
define a mixed strategy which is staring in the direct mode and then
switching to the reverse mode when the storage becomes a problem (see
section 8.3).




Next: An alternative: the single
Up: Mathematical background
Previous: Principle
Contents
Jean-Pierre Merlet
2012-12-20
![]() . We have defined
two types of order for a given set of boxes
. We have defined
two types of order for a given set of boxes ![]() :
:
![]() by the
by the
![]() having the lowest
having the lowest ![]() but instead of adding the remaining
but instead of adding the remaining ![]()
![]() at the end of the list
at the end of the list ![]() we shift by
we shift by ![]() the
boxes in the list, thereby freeing the storage of
the
boxes in the list, thereby freeing the storage of
![]() which is used to store the remaining
which is used to store the remaining ![]()
![]() . In other words we may consider the solving procedure as
finding a leaves in a tree which are solutions of the problem: in the
Direct Storage mode we may jump during the bisection from one
branch of the tree to another while in the Reverse storage mode
we examine all the leaves issued from a branch of
the tree before examining the other branches of the tree. If we are
looking for all the solutions the storage mode has no influence on the
total number of boxes that will be examined. But the Reverse
Storage mode may have two advantages:
. In other words we may consider the solving procedure as
finding a leaves in a tree which are solutions of the problem: in the
Direct Storage mode we may jump during the bisection from one
branch of the tree to another while in the Reverse storage mode
we examine all the leaves issued from a branch of
the tree before examining the other branches of the tree. If we are
looking for all the solutions the storage mode has no influence on the
total number of boxes that will be examined. But the Reverse
Storage mode may have two advantages: