



Next: Managing the bisection and
Up: Mathematical background
Previous: Mathematical background
Contents
Let
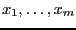 be the set of unknowns and
let
be the set of unknowns and
let
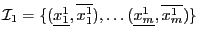 be the set of
be the set of 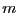 intervals in which you are searching the solutions
of the
intervals in which you are searching the solutions
of the  equations
equations
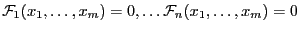 (for the sake of simplicity we don't consider
inequalities but the extension to inequalities is straightforward).
(for the sake of simplicity we don't consider
inequalities but the extension to inequalities is straightforward).
We will denote by 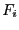 the interval value of
the interval value of 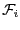 when this
function is evaluated for the box
when this
function is evaluated for the box
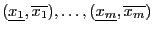 of the unknowns while
of the unknowns while 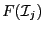 will denote the
will denote the
 -dimensional interval vector constituted of the
-dimensional interval vector constituted of the 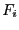 when the
unknowns have the interval value defined by the set
when the
unknowns have the interval value defined by the set 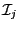 .
.
The algorithm will use a list of boxes 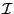 whose maximal size
whose maximal size 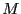 is an
input of the program. This list is initialized with
is an
input of the program. This list is initialized with 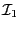 . The
number of
. The
number of 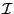 currently in the list is
currently in the list is 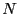 and therefore at the
start of the program
and therefore at the
start of the program 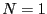 . The algorithm will also use an accuracy on
the variable
. The algorithm will also use an accuracy on
the variable 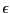 and on the functions
and on the functions 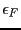 . The norm of a
. The norm of a 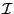 is defined as:
is defined as:
The norm of the interval vector 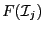 is defined as:
is defined as:
The algorithm uses an index 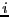 and the result is a
set
and the result is a
set 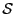 of interval vector
of interval vector 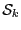 for the unknowns whose size is
for the unknowns whose size is 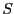 .
We assume that there is no
.
We assume that there is no 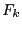 with
with 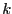 in
in ![$[1,n]$](img11.png) such that
such that
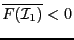 or
or
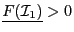 ,
otherwise the equations have no solution in
,
otherwise the equations have no solution in 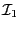 .
Two lists of interval vectors
.
Two lists of interval vectors
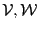 whose size
is
whose size
is 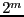 will also be used.
The algorithm is initialized with
will also be used.
The algorithm is initialized with 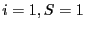 and proceed along the following steps:
and proceed along the following steps:
- if
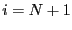 return
return 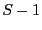 and
and 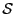 and exit
and exit
- bisect
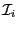 which produce
which produce 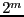 new interval vectors
new interval vectors
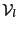 and set
and set 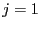
- for
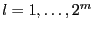
- evaluate
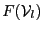
- if it exist
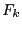 with
with 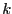 in
in ![$[1,n]$](img11.png) such that
such that
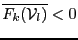 or
or
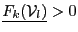 ,
then
,
then
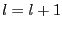 and go to step 3
and go to step 3
- if
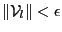 or
or
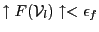 , then store
, then store 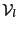 in
in 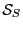 , increment
, increment 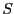 and go to step 3
and go to step 3
- store
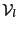 in
in 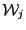 , increment
, increment 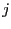 and go
to step 3
and go
to step 3
- if
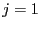 increment
increment 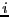 and go to step 1
and go to step 1
- if
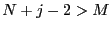 return a failure code as there is no space
available to store the new intervals
return a failure code as there is no space
available to store the new intervals
- if
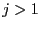 store one of the
store one of the 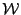 in
in 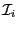 , the other
, the other
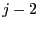 at the end of
at the end of 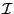 , starting at position
, starting at position 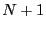 . Add
. Add 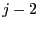 to
to 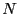 and go to step 1
and go to step 1
Basically the algorithm just bisect the box until either
their width is lower than 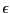 or the width of the interval
function is lower than
or the width of the interval
function is lower than 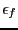 (provided that there is enough
space in the list to store the intervals). Then if all the intervals
functions contain 0 we get a new solution, if one of them does not
contain 0 there is no solution of the
equations within the current box. A special case occurs
when all the components of the box are reduced to a point, in which case a
solution is obtained if the absolute value of the interval evaluation
of the function is lower than
(provided that there is enough
space in the list to store the intervals). Then if all the intervals
functions contain 0 we get a new solution, if one of them does not
contain 0 there is no solution of the
equations within the current box. A special case occurs
when all the components of the box are reduced to a point, in which case a
solution is obtained if the absolute value of the interval evaluation
of the function is lower than 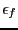 .
.
Now three problems have to be dealt with:
- how to choose the
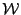 which will be put in place of the
which will be put in place of the
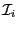 and in which order to store the other
and in which order to store the other 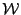 at the
end of the list?
at the
end of the list?
- can we improve the management of the bisection process in order
to conclude the algorithm with a limited number
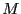 ?
?
- how do we distinguish distinct solutions ?
The first two problems will be addressed in the next section.




Next: Managing the bisection and
Up: Mathematical background
Previous: Mathematical background
Contents
Jean-Pierre Merlet
2012-12-20
![]() be the set of unknowns and
let
be the set of unknowns and
let
![]() be the set of
be the set of ![]() intervals in which you are searching the solutions
of the
intervals in which you are searching the solutions
of the ![]() equations
equations
![]() (for the sake of simplicity we don't consider
inequalities but the extension to inequalities is straightforward).
(for the sake of simplicity we don't consider
inequalities but the extension to inequalities is straightforward).
![]() the interval value of
the interval value of ![]() when this
function is evaluated for the box
when this
function is evaluated for the box
![]() of the unknowns while
of the unknowns while ![]() will denote the
will denote the
![]() -dimensional interval vector constituted of the
-dimensional interval vector constituted of the ![]() when the
unknowns have the interval value defined by the set
when the
unknowns have the interval value defined by the set ![]() .
.
![]() whose maximal size
whose maximal size ![]() is an
input of the program. This list is initialized with
is an
input of the program. This list is initialized with ![]() . The
number of
. The
number of ![]() currently in the list is
currently in the list is ![]() and therefore at the
start of the program
and therefore at the
start of the program ![]() . The algorithm will also use an accuracy on
the variable
. The algorithm will also use an accuracy on
the variable ![]() and on the functions
and on the functions ![]() . The norm of a
. The norm of a ![]() is defined as:
is defined as: