



Next: Solutions and Distinct solutions
Up: Mathematical background
Previous: Managing the bisection and
Contents
An alternative: the single bisection
A possibility to reduce the combinatorial explosion of the previous
algorithm is to bisect not all the variables i.e. to use the
full bisection mode, but only one of
them (it must be noted that the algorithms in ALIAS will not
accept a full bisection mode if the number of unknowns exceed
10). This may reduce the computation time as the number of function
evaluation may be reduced. But the problem is to determine which
variable should be bisected. All the solving algorithms of ALIAS
may manage this single bisection by setting the flag Single_Bisection to a value different from 0.
The value of this global variable indicates various bisection modes.
Although the behavior of the
mode may change according to the algorithm here are the
possible modes for the general solving algorithm and the corresponding
values for Single_Bisection:
- 1 : we just split the variable having
the largest width (valid for all algorithms). Note however that it is
still possible to order the bisection i.e. to split first a subset of
the unknowns until their width is small (i.e. lower than
ALIAS_Accuracy, then another subset and so
on. This is obtained by setting flag
ALIAS_Ordered_Bisection
to 1 and
defining an integer matrix ALIAS_Order_Bisection
whose rows
indicate the bisected subset and
should end by 0. For example if this matrix has as rows
[1,3,0],[2,4,5,0], then the algorithm will first bisect the unknowns 1
and 3 until their width is small, then the unknowns 2,4,5. If all
unknowns indicated in the rows of the matrix have a small width, then
the bisection algorithm revert to the normal behavior.
- 2: to determine the variable that will be bisected we use the following
approach: we compute the order criteria for the two boxes
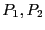 that will result from the bisection of variable
that will result from the bisection of variable 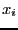 and retain the lowest
criteria
and retain the lowest
criteria 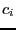 . The variable that will be bisected is the one that has the
lowest
. The variable that will be bisected is the one that has the
lowest 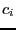 except if for at least one variable the interval
evaluation of the function for
except if for at least one variable the interval
evaluation of the function for 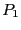 or
or 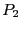 does not contain 0. In
that case the variable that will be bisected is the one that
verify the previous property and which has the lowest
does not contain 0. In
that case the variable that will be bisected is the one that
verify the previous property and which has the lowest 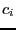 among all
the input intervals having the property.
However to avoid bisecting over and over
the same variable we use another test: let
among all
the input intervals having the property.
However to avoid bisecting over and over
the same variable we use another test: let 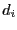 be the width of the
interval
be the width of the
interval
![$[\underline{x_i},\overline{x_i}]$](img116.png) and
and 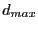 be the
maximum of all the
be the
maximum of all the 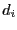 . If
. If
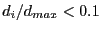 we don't consider the
variable
we don't consider the
variable 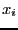 as a possible bisection direction.
It is also possible to mix this mode with mode 1. If the integer
variable ALIAS_RANDG is set to a strictly positive value then
ALIAS_RANDG bisection will be performed using mode 2 while the
next bisection will be performed using mode 1 and the process will be
repeated
as a possible bisection direction.
It is also possible to mix this mode with mode 1. If the integer
variable ALIAS_RANDG is set to a strictly positive value then
ALIAS_RANDG bisection will be performed using mode 2 while the
next bisection will be performed using mode 1 and the process will be
repeated
- 3, 4 : similar to 1
- 5 : we use a round-robin mode i.e. each variable is
bisected in turn (first
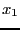 , then
, then 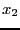 and so on) unless the width
of the input intervals is less than the desired accuracy on the
variable, in which case the bisected variable is the next one having a
sufficient width (valid for all algorithms)
The flag ALIAS_Round_Robin is used to indicate at each
bisection which variable should be bisected.
and so on) unless the width
of the input intervals is less than the desired accuracy on the
variable, in which case the bisected variable is the next one having a
sufficient width (valid for all algorithms)
The flag ALIAS_Round_Robin is used to indicate at each
bisection which variable should be bisected.
- 6: we emulate the smear function (see section 2.4.1.3)
with an estimation of the
gradient based on finite difference (procedure
Select_Best_Direction_Grad)
- 7: here again we use the flag
ALIAS_Ordered_Bisection
set to 1 and
defining an integer matrix ALIAS_Order_Bisection
whose rows indicates an order for bisecting the unknowns. The largest
variable in the first row will be bisected first and so on until all
the variables in a row have a width lower than
ALIAS_Accuracy. We then proceed to the second row.
As soon as all variables in all rows have a width lower than
ALIAS_Accuracy we use the bisection 1.
- 20: the user has defined its own bisection procedure, see
section 11.3
For all general purpose solving procedures the number of the variable
that has been
bisected is available in the integer
ALIAS_Selected_For_Bisection.
There is another mode called the mixed bisection: among the  variables we will bisect
variables we will bisect 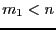 variables, which will lead to
variables, which will lead to
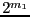 new boxes. This mode is obtained by setting
the global integer variable
new boxes. This mode is obtained by setting
the global integer variable
ALIAS_Mixed_Bisection
to 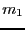 . Whatever is the value of
Single_Bisection we will order the variables according to their width
and select the
. Whatever is the value of
Single_Bisection we will order the variables according to their width
and select the 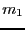 variables having the largest width.
variables having the largest width.




Next: Solutions and Distinct solutions
Up: Mathematical background
Previous: Managing the bisection and
Contents
Jean-Pierre Merlet
2012-12-20
![]() variables we will bisect
variables we will bisect ![]() variables, which will lead to
variables, which will lead to
![]() new boxes. This mode is obtained by setting
the global integer variable
new boxes. This mode is obtained by setting
the global integer variable
![]() . Whatever is the value of
Single_Bisection we will order the variables according to their width
and select the
. Whatever is the value of
Single_Bisection we will order the variables according to their width
and select the ![]() variables having the largest width.
variables having the largest width.