Using SHASTA from within MAPLE

It is possible to use MAPLE as a front end to SHASTA, provided that the SHASTA executable is in your path and that the file shasta.m is in the MAPLE library path (you can use the libname variable within MAPLE to ensure the latter). After loading the MAPLE-SHASTA interface via the with(shasta) command, the following functions are available: adjoint, apply, decompose, dispersion, efactor, eigenring, exteriorPower, hyper, leftGcd, leftLcm, Loewy, makeIntegral, mult, normalize, polynomialKernel, polynomialSolution, rationalKernel, rationalSolution, rightGcd, rightLcm, rightQuotient, sections and spread. 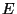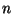All those functions take the same arguments than their SHASTA analogues, plus the two symbols $E$ and $n$ that you use for the shift and independent variable respectively. For example, where you would use

-> L2 := exteriorPower(E^3 - n, 2)

in SHASTA, use

> L2 := exteriorPower(E^3 - n, 2, E, n)

from within MAPLE. See the sample MAPLE worksheet that is provided with SHASTA for more details. Note that in order not to conflict with the factor and linalg[kernel] functions in MAPLE, the functions factor and kernel of SHASTA are provided under MAPLE under the names efactor, polynomialKernel and rationalKernel. Note also that the functions decompose, efactor, eigenring, polynomialSolution and rationalSolution do some additional processing of the output of SHASTA when called from within MAPLE (see the corresponding reference pages for details).