decompose

Next: degree Up: Supported functions Previous: coefficient Contents Index

decompose

Usage

decompose L

Parameter Type Description

L ${\mathbb{Q}}[n,E]$ A difference operator of order at most 3

Parameter	Type	Description
L	${\mathbb{Q}}[n,E]$	A difference operator of order at most 3

Description

Returns one of the following possible results:

(i): L, in which case L cannot be written as a least common left multiple of lower order operators (L can still be either reducible or irreducible in that case).
(ii): $[L_1,\dots,L_m]$ where $L_i \in {\mathbb{Q}}(n)[E]$ , in which case L is a least common left multiple of $L_1,\dots,L_m$ .
(iii): $[h(n),a(n,E),b(n,E),f_1(n,E),\dots,f_m(n,E)]$ , where $h(n) \in {\mathbb{Q}}[n]$ is irreducible and ,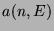
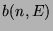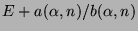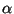, $f_1(n,E),\dots,f_m(n,E) \in {\mathbb{Q}}(n)[E]$ , in which case L is a least common left multiple of $f_1(n,E),\dots,f_m(n,E)$ and of $E + a(\alpha, n) / b(\alpha, n)$ where $\alpha$ ranges over all the roots of .

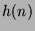Example

We decompose the difference equation

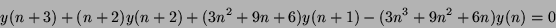$\begin{displaymath} y(n+3)+(n+2)y(n+2)+(3n^2+9n+6)y(n+1)-(3n^3+9n^2+6n)y(n) = 0 \end{displaymath}$

(1)

as follows:

1 --> L := E^3+(n+2)*E^2+(3*n^2+9*n+6)*E-3*n^3-9*n^2-6*n;
2 --> v := decompose(L);
3 --> tex(v);

$\begin{displaymath} \left[ n^{3}-2\,n^{2}+4\,n-6 , \left(-n+1\right)\,E , 1 \right] \end{displaymath}$

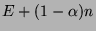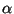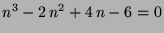This means that the operator of (1) is a least common left multiple of $E + (1-\alpha) n$ where $\alpha$ ranges over the roots of $n^{3}-2\,n^{2}+4\,n-6 = 0$ .

Usage within MAPLE

When using decompose from inside MAPLE, the result returned from SHASTA is further transformed into one of the following:

(i): L, in which case L cannot be written as a least common left multiple of lower order operators.
(ii): An object of the form LeftLcm $(L_1,\dots,L_m)$ where the 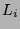's are difference operators, in which case L is a least common left multiple of $L_1,\dots,L_m$ .
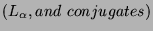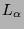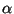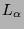(iii): An object of the form LeftLcm $(L_\alpha, and~conjugates)$ where $L_\alpha$ is a difference operator containing an algebraic number $\alpha$ , in which case L is a least common left multiple of all the conjugates of $L_\alpha$ .

So the above example in MAPLE would be:

> L := E^3+(n+2)*E^2+(3*n^2+9*n+6)*E-3*n^3-9*n^2-6*n;
> decompose(L, E, n);

$\begin{displaymath} {\it LeftLcm}(E+\left (-{\it RootOf}({{\it\_Z}}^{3}-2\,{{\it... ...{2 }+4\,{\it\_Z}-6)+1\right )n,\mbox {{\tt \lq and conjugates\lq }}) \end{displaymath}$

See Also

factor,Loewy

Next: degree Up: Supported functions Previous: coefficient Contents Index

Manuel Bronstein 2002-09-04