3rd Step : 1D features matching

model invariant by rotations and translations

As for the first step, missing catorgaphic data are modelled by a null label$\emptyset$.
 
 

Second order potentials

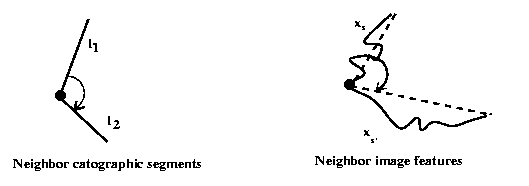
The potentials on the cliques of order 2 induce some constraints on the consistency of angles between neighboring chains and the corresponding map segments :

1) two chains matched to the same segments should make an angle  close to PI.

2) two connected chains matched to two connected segments should have an angle close to the corresponding segments.

3) two connected chains matched to two non connected segments are penalized.
 
 

$$V_c(x_s,x_{s'})=\left\lbrace\begin{array}{l}\alpha _1\t......mptyset \mbox{ ou } f(x_{s'})=\emptyset\\\end{array} \right.$$

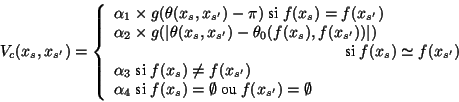
The function g is defined on $[-2\pi,2\pi]$, convex and minimum in 0 ;  g drives the strength of the prior on angles. We consider a parabolic function.
 
 

Third order potentials

The potentials associated with the third order cliques allow us to avoid some label continuity breaks:

$$V_c(x_s,x_{s'},x_{s''})= \left\lbrace\begin{array}{l}\bet......_s)\not=f(x_{s'})\\0 \mbox{ sinon } \\\end{array} \right.$$

 
 
 

Data attachment term

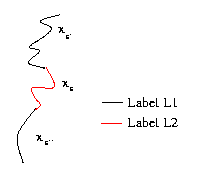
This last term adds some consistency constraints between the length of the chains and the corresponding segments.

It is defined using the features length:
 
 

$$\sum_{i(labels)}[\sum_{s(sites)} l(x_s) \delta_{f(x_s)=i}-l_i]^2$$

This term induces non markovian properties as it includes all sites of the models. However, we still have a Gibbs distribution.
 

The energy is minimized by a simulated annealing using a Metropolis dynamics but we can also use an ICM because the first step (pixel labelling) provides a good initialization. This last algorithm is faster than the simulated annealing.
 

November 1998