Potentials corresponding to this first step (Markov model)

The data attachment (first order) term is defined by the distance between two nodes (i.e. the distance between a pixel of the image and a segment of the map).

We add a null label $\emptyset$ on the map  to model the missing cartographic data.

This label is located within a constant distance d, w.r.t. all the nodes.

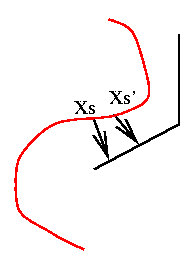
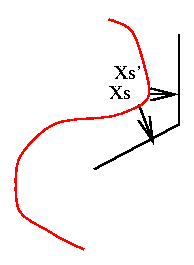
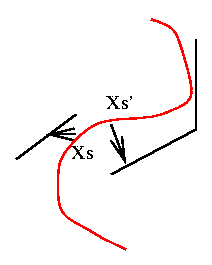
The potentials w.r.t. order 2 cliques yield homogeneity constraints:
 

$$V_c(x_s,x_{s'})=\left\lbrace\begin{array}{l}0 \mbox{ if......meq f(x_{s'})\\\alpha _2 \mbox{ otherwise }\end{array} \right.$$

	$$V_C(x_s,x_{s'})=\alpha_1$$	$$V_C(x_s,x_{s'})=\alpha_2$$

$$0<\alpha_1<\alpha_2$$

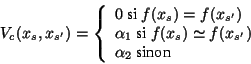
The potentials w.r.t. order 1 cliques represent the data attachment term:

Distance between the pixel and the label (cartographic segment)

 

The energy defined by the sum over all the potentials is minimised using simulated annealing with a Metropolis dynamics.
 
 

Octobre 1998