|
Solving polynomial equations
|
The first type of problems that we consider is the solution of polynomial equations:
where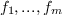 
are polynomials in the variables 
with coefficients in the field 
.
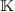Let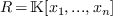 
be the ring of such polynomials and let
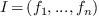be the ideal of 
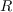generated by these polynomials 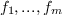. The algebraic
approach to solve the system of equations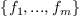 
proceeds in two steps:
Compute the ring structure of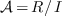 
represented
by a (monomial) basis and the operators of multiplication by the
variables.
Compute the roots of the system from the operators of
multiplication by the variables, when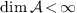 
.
We detail these main steps hereafter.