

|
Border bases
|
Border basis algorithms provide an efficient way to compute the ring
structure of  , which is represented by
, which is represented by
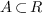 a vector space of polynomials, which
corresponds to the normal form of the elements of the equivalent
classes of
a vector space of polynomials, which
corresponds to the normal form of the elements of the equivalent
classes of 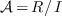 ,
,
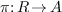 a projection onto
a projection onto 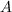 ,
with kernel
,
with kernel 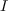 , which computes the normal
form of the elements of
, which computes the normal
form of the elements of 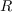 modulo the ideal
modulo the ideal
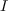 .
.
This means that we have the exact sequence:
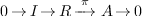
with 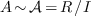 . Normal form algorithms compute an
explicit basis (usually a monomial set) of
. Normal form algorithms compute an
explicit basis (usually a monomial set) of 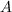 and
an effective projection (usually a reduction process).
and
an effective projection (usually a reduction process).
Celebrate Gröbner basis computation provides such a normal form. Border basis is also a normal form algorithm, which generalizes Gröbner basis.
Assume that 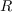 is graded by a ordered additive
monoïd that we denote
is graded by a ordered additive
monoïd that we denote 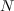 (for instance
(for instance 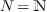 if we use the classical notion of degree): there
exists a degree function
if we use the classical notion of degree): there
exists a degree function 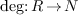 such that for any
such that for any
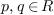 ,
, 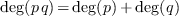 .
.
The set of monomials of 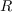 is denoted
is denoted 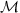 . For
. For 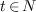 , let
, let  be the vector space spanned by the set
be the vector space spanned by the set 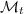 monomials of degree
monomials of degree 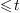 .
.
A border basis is defined with respect to a set 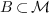 of monomials, connected to
of monomials, connected to 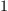 (if
(if 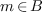 either
either 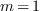 or
or 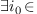 and
and 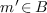 such that
such that 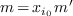 ). Let
). Let
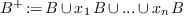 and
and 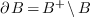 . The computation
of a border basis goes through the construction of a family
. The computation
of a border basis goes through the construction of a family 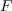 of polynomials of the form
of polynomials of the form
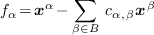
which are in 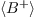 with only one term denoted
with only one term denoted 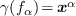 in
in 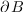 . We illustrate it in
the following picture:
. We illustrate it in
the following picture:

The basis 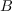 corresponds to the light blue
region. The monomial in
corresponds to the light blue
region. The monomial in 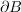 are the thick points.
For
are the thick points.
For 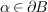 , there is a polynomial
, there is a polynomial 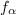 with one monomial
with one monomial 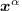 in
in 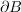 (e.g. the red thick point) and all the other monomials of its support
are in the light blue region
(e.g. the red thick point) and all the other monomials of its support
are in the light blue region 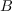 . The polynomials
. The polynomials
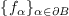 can be used to rewrite all polynomials in
can be used to rewrite all polynomials in 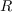 as linear combinations of elements in
as linear combinations of elements in 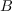 modulo the ideal
modulo the ideal 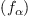 .
.
A family of polynomials 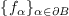 of this form is called
a rewriting family. The family is graded if
of this form is called
a rewriting family. The family is graded if 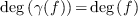 for all
for all 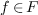 . For
. For 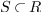 ,
, 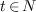 ,
, 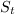 is the
set of elements of
is the
set of elements of 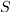 of degree
of degree 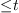 .
.
A rewriting family 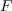 is said to be
complete in degree
is said to be
complete in degree 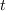 if it is graded
and satisfies
if it is graded
and satisfies 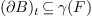 ; that is, each monomial
; that is, each monomial 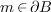 of degree at most
of degree at most 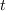 is the
leading monomial of some (necessarily unique)
is the
leading monomial of some (necessarily unique) 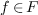 .
.
Given a rewriting family 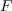 which is complete in
degree
which is complete in
degree 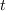 , we define recursively the projection
, we define recursively the projection
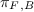 on
on 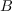 along
along 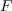 in the following way:
in the following way: 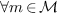 ,
,
if 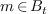 , then
, then 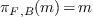 ,
,
if 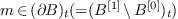 , then
, then 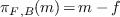 , where
, where
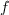 is the (unique) polynomial in
is the (unique) polynomial in 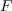 for which
for which 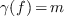 ,
,
if 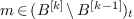 for some integer
for some integer  ,
write
,
write 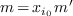 , where
, where 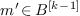 and
and
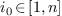 is the smallest possible variable index
for which such a decomposition exists, then
is the smallest possible variable index
for which such a decomposition exists, then 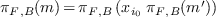 .
.
The map πF,B extends by linearity to a linear map from
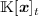 onto
onto 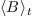 . By construction,
. By construction,
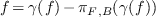 and
and 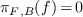 for all
for all 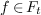 .
.
The next theorem [?] shows that, under some
natural commutativity condition, the map 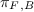 coincides with the linear projection from
coincides with the linear projection from 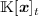 onto
onto
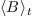 along the vector space
along the vector space 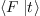 :
:
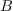 is connected to
is connected to 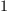 and let
and let 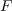 be a rewriting family for
be a rewriting family for 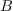 , complete in degree
, complete in degree 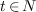 . Suppose
that, for all
. Suppose
that, for all 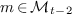 ,
,
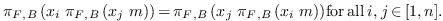
(1)
Then 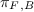 coincides with the linear projection
of
coincides with the linear projection
of  on
on 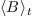 along the
vector space
along the
vector space 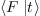 ; that is,
; that is, 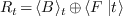 .
.
The commutation polynomials or 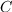 -polynomials are
the polynomials
-polynomials are
the polynomials 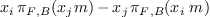 for
for 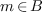 ,
,
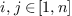 such that
such that 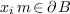 or
or 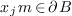 . By this theorem,
. By this theorem, 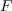 is a border
basis for
is a border
basis for 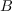 in degree
in degree 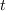 iff all the
iff all the 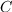 -polynomials reduces to
-polynomials reduces to 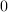 , i.e. their image by
, i.e. their image by 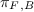 is
is 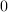 .
.
The border basis algorithm computes a rewriting family 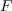 which satisfies the relation (?) for any
degree
which satisfies the relation (?) for any
degree 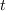 [?]. It proceeds
incrementally degree by degree with a candidate monomial set
[?]. It proceeds
incrementally degree by degree with a candidate monomial set 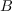 for the basis of
for the basis of  and the
rewriting family
and the
rewriting family 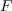 for
for 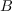 at a given degree
at a given degree 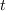 . At each degree, the
non-zero polynomials deduced from the relations (?) are
added to
. At each degree, the
non-zero polynomials deduced from the relations (?) are
added to 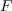 .
.
In the main loop of the algorithm, the following operations are performed:
prolongation: determine the new elements of 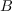 in degree
in degree  and the elements
and the elements
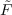 of
of 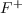 which are in
which are in
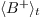 ;
;
matrix construction: compute the coefficient matrix 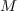 of
of 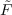 with respect to
with respect to  ;
;
linear reduction: compute a (sparse) 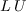 decomposition of the matrix
decomposition of the matrix 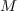 and update the
rewriting family
and update the
rewriting family 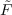 ;
;
commutation reduction: reduce the 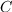 -polynomials
with respect to
-polynomials
with respect to 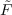 and update
and update 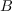 ,
, 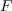 and
and 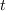 ;
;
This loop is iterated until a complete rewriting family for 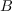 which satisfies (?) is obtained in the case
of a zero-dimensional ideal or until the Gotzmann regularity criterion
is satisfied [?]. The computation is controlled by a
choice function, which select “leading” monomials for the
construction of rewriting families.
which satisfies (?) is obtained in the case
of a zero-dimensional ideal or until the Gotzmann regularity criterion
is satisfied [?]. The computation is controlled by a
choice function, which select “leading” monomials for the
construction of rewriting families.
Let 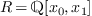 . We consider the following polynomial
system:
. We consider the following polynomial
system:
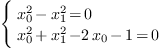
The computed border basis for the monomial basis 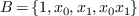 is
is
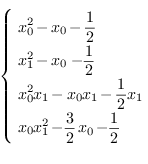
The matrices of multiplication by 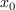 ,
,
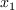 in this basis are
in this basis are
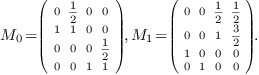
The computation of a Gröbner basis for the degree reverse
lexicographic monomial ordering with 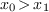 yields
the same basis
yields
the same basis 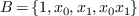 and thus the same matrices of
multiplications by the variables
and thus the same matrices of
multiplications by the variables 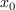 ,
, 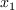 .
.
Consider now a small perturbation of the polynomial system:
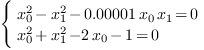
The computed border basis is

for the same monomial basis 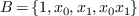 . The matrices of
multiplication by
. The matrices of
multiplication by 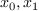 in this basis are
in this basis are
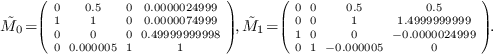
These matrices are small perturbations of the multiplication matrices of the initial system. The order of the perturbation is the same as the order of the perturbation of the polynomial system.
If we compute a Gröbner basis for the degree reverse
lexicographic monomial ordering with 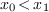 , we
obtain the basis
, we
obtain the basis 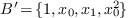 and the numerical
approximation (within
and the numerical
approximation (within 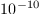 ) of the matrices of
multiplication by the variables
) of the matrices of
multiplication by the variables 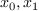 in this basis
are
in this basis
are
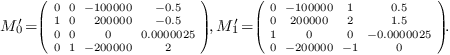
We observe a great variation in the magnitude of the coefficients (of the order the inverse of the magitude of the perturbation in this example, but it could be worth!).
This illustrates the numerical stability of border basis computation and the instability of Gröbner basis computation against perturbations of the coefficients of the polynomial system.
[1] B. Mourrain and P. Trébuchet. Generalized normal forms and polynomials system solving. In M. Kauers, editor, ISSAC 2005: Proceedings of the ACM SIGSAM International Symposium on Symbolic and Algebraic Computation, pages 253–260. 2005.
[2] B. Mourrain and Ph. Trébuchet. Border basis representation of a general quotient algebra. In J. van der Hoeven, editor, ISSAC 2012, pages 265–272. Jul 2012.