Another commonly used normalization is to set F=1. If we use the same notations as in the last subsection, the problem becomes to minimize the following function:
where 
is the sixth element of vector 
, i.e., 
.
Indeed, we seek for a least-squares solution to 
under
the constraint 
. The equation can be rewritten as
where 
is the matrix formed by the first (n-1) columns of
, 
is the last column of and 
is the
vector 
. The problem can now be solved by the technique
described in sect:Ax=b.
In the following, we present another technique for solving this kind of problems, i.e.,
based on eigen analysis, where we consider a general formulation, that is
is a 
matrix, is a m-vector, and 
is the
last element of vector . The function to minimize is
As in the last subsection, the symmetric matrix 
can be decomposed as
in (5), i.e., 
. Now if
we normalize each eigenvalue and eigenvector by the last element of the
eigenvector, i.e.,
where 
is the last element of the eigenvector 
, then the
last element of the new eigenvector 
is equal to one. We now have
where 
and
.
The original problem (7) becomes:
Findsuch that
is minimized with
subject to
.
After some simple algebra, we have
The problem now becomes to minimize the following unconstrained function:
where 
is the Lagrange multiplier. Setting the derivatives of 
with respect to 
through 
and yields:
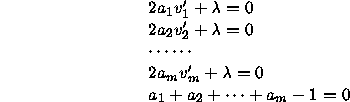
The unique solution to the above equations is given by
where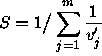 
.
The solution to the problem (7) is given by
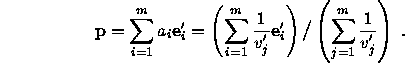
Note that this normalization (F=1) has singularities for all conics going through the origin. That is, this method cannot fit such conics because they require to set F=0. This might suggest that the other normalizations are superior to the F=1 normalization with respect to singularities. However, as shown in [20], the singularity problem can be overcome by shifting the data so that they are centered on the origin, and better results by setting F=1 has been obtained than by setting A+C=1.
