Normalization with

 

Let . As , i.e., the sum of squared coefficients, can never be zero for a conic, we can set to remove the arbitrary scale factor in the conic equation. The system equation becomes

where .

Given n points, we have the following vector equation:

where . The function to minimize becomes:

 

where is a symmetric matrix. The solution is the eigenvector of corresponding to the smallest eigenvalue (see below).

Indeed, any symmetric matrix (m=6 in our case) can be decomposed as

 

with

where is the i-th eigenvalue, and is the corresponding eigenvector. Without loss of generality, we assume . The original problem (4) can now be restated as:

Find such that is minimized with

subject to .

After some simple algebra, we have

The problem now becomes to minimize the following unconstrained function:

where is the Lagrange multiplier. Setting the derivatives of J with respect to through and yields:

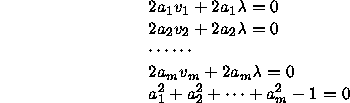
There exist m solutions. The i-th solution is given by

The value of corresponding to the i-th solution is

Since , the first solution is the one we need (the least-squares solution), i.e.,

Thus the solution to the original problem (4) is the eigenvector of corresponding to the smallest eigenvalue.