The least-squares method described in the last sections is usually called ordinary least-squares estimator (OLS). Formally, we are given n equations:
where 
is the additive error in the i-th equation with mean
zero: 
, and variance 
.
Writing down in matrix form yields
where
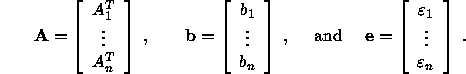
The OLS estimator tries to estimate 
by minimizing the following sum
of squared errors:
which gives, as we have already seen, the solution as
It can be shown (see, e.g., [2]) that the OLS estimator produces
the optimal estimate of , ``optimal'' in terms of minimum
covariance of , if the errors are uncorrelated
(i.e., 
) and their
variances are constant (i.e., 
).
Now let us examine whether the above assumptions are valid or not for conic
fitting. Data points are provided by some signal processing algorithm such as
edge detection. It is reasonable to assume that errors are independent from
one point to another, because when detecting a point we usually do not use any
information from other points. It is also reasonable to assume the errors are
constant for all points because we use the same algorithm for edge detection.
However, we must note that we are talking about the errors in the points,
but not those in the equations (i.e., ). Let the error in
a point 
be Gaussian with mean zero and covariance
, where 
is the 2 
2 identity
matrix. That is, the error distribution is assumed to be isotropic in both
directions ( 
, 
).
In sec:Kalman, we will consider the case where each point may have
different noise distribution. Refer to eq:A+C=1. We now compute the
variance 
of function 
from point 
and
its uncertainty. Let 
be the true position of the
point, we have certainly
We now expand into Taylor series at 
and 
,
i.e.,
Ignoring the high order terms, we can now compute the variance of , i.e.,
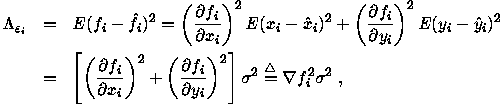
where 
is just the gradient of with respect to 
and
, and
It is now clear that the variance of each equation is not the same, and thus the OLS estimator does not yield an optimal solution.
In order to obtain a constant variance function, it is sufficient to divide the original function by its gradient, i.e.,
then 
has the constant variance 
. We can now try to find the
parameters by minimizing the following function:
where 
. This method is thus called Gradient Weighted Least-Squares,
and the solution can be easily obtained by setting 
, which yields
Note that the gradient-weighted LS is in general a nonlinear minimization
problem and a closed-form solution does not exist. In the above, we gave a
closed-form solution because we have ignored the dependence of 
on
in computing 
. In reality, does
depend on , as can be seen in eq:derive. Therefore, the above
solution is only an approximation. In practice, we run the following iterative
procedure:
In the above, the superscript (k) denotes the iteration number.
