![]() que l'on puisse atteindre un espace de travail voulue
que l'on puisse atteindre un espace de travail voulue
![]() qu'il puisse exercer une force minimale quelle que soit sa position, alors
que les moteurs électriques ont un couple limité
qu'il puisse exercer une force minimale quelle que soit sa position, alors
que les moteurs électriques ont un couple limité
![]() que la précision du robot soit au moins égale à une
valeur donnée quelle que soit sa position alors que les capteurs
fournissent une mesure inexacte
que la précision du robot soit au moins égale à une
valeur donnée quelle que soit sa position alors que les capteurs
fournissent une mesure inexacte
![]() que la vitesse minimale du robot ne soit pas inférieure à
un certain seuil, alors que les moteurs ont une vitesse de rotation limitée
que la vitesse minimale du robot ne soit pas inférieure à
un certain seuil, alors que les moteurs ont une vitesse de rotation limitée
![]() ....
....
L'idée
![]() chaque critère
chaque critère ![]() est quantifié par un nombre qui est 0 si le critère satisfait
la contrainte du cahier des charges
est quantifié par un nombre qui est 0 si le critère satisfait
la contrainte du cahier des charges
![]() on construit une fonction de coût F
qui est minimale si toutes les contraintes
du cahier des charges sont vérifiées:
on construit une fonction de coût F
qui est minimale si toutes les contraintes
du cahier des charges sont vérifiées:
![]() on utilise une procédure numérique
d'optimisation
qui va essayer de déterminer les dimensions du robot qui minimise
F
on utilise une procédure numérique
d'optimisation
qui va essayer de déterminer les dimensions du robot qui minimise
F
mais cela a des inconvénients:
![]() les critères ont différentes unités
les critères ont différentes unités ![]() les résultats sont très dépendants des poids w
les résultats sont très dépendants des poids w
![]() certains critères sont antagonistes
certains critères sont antagonistes ![]() les résultats sont très dépendants des poids w
les résultats sont très dépendants des poids w
![]() il faut savoir évaluer très rapidement les valeurs des critères
il faut savoir évaluer très rapidement les valeurs des critères
![]() la procédure est très longue si le nombre de paramètres
à déterminer est important
la procédure est très longue si le nombre de paramètres
à déterminer est important
![]() problème des minima locaux
problème des minima locaux
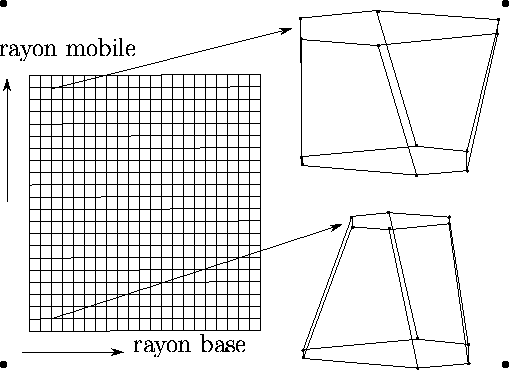
Un point de cet espace représente une géométrie unique du robot
![]() le robot "optimal" sera contenu dans l'intersection
de toutes les régions
le robot "optimal" sera contenu dans l'intersection
de toutes les régions ![]()
un exemple: l'espace
des paramètres est de dimension 2:
![]() le rayon R du plateau
de base
le rayon R du plateau
de base
![]() le rayon r du plateau mobile
le rayon r du plateau mobile
![]() les longueurs des jambes doivent être entre
les longueurs des jambes doivent être entre![]()
Le problème est de déterminer quelles sont
les valeurs possibles de r, R
pour qu'en une position donnée P
du plateau les longueurs des jambes soient bien dans [![]() ]
]
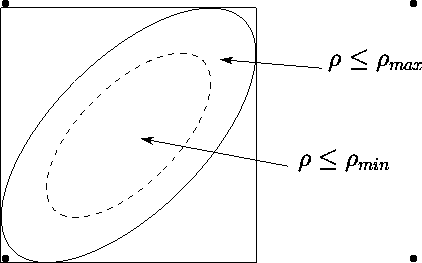
![]() tous les (r,R)
tels qu'en P on ait
tous les (r,R)
tels qu'en P on ait ![]() sont à l'intérieur d'une ellipse
sont à l'intérieur d'une ellipse
![]() tous les (r,R)
tels qu'en P on ait
tous les (r,R)
tels qu'en P on ait ![]() sont à l'extérieur d'une autre
ellipse
sont à l'extérieur d'une autre
ellipse
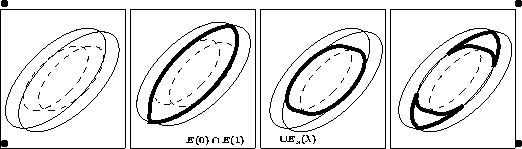
on peut généraliser le résultat
au cas où l'on ne considère plus un seul point mais un segment
de trajectoire ![]()
![]() tous les (r,R)
tels que sur
tous les (r,R)
tels que sur ![]() on ait
on ait ![]() sont à l'intérieur d'une union d'ellipse
U1
sont à l'intérieur d'une union d'ellipse
U1
![]() tous les (r,R)
tels que sur
tous les (r,R)
tels que sur ![]() on ait
on ait ![]() sont à l'extérieur d'une autre
union
d'ellipse U2
sont à l'extérieur d'une autre
union
d'ellipse U2
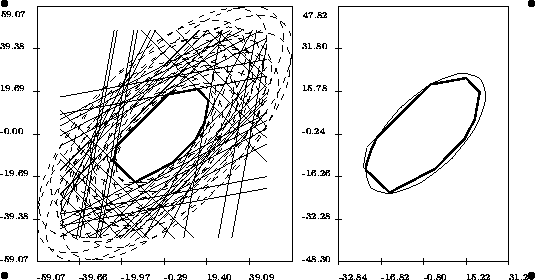
![]() il suffit alors de soustraire U2 à U1 pour obtenir la région
pour laquelle on a toujours
il suffit alors de soustraire U2 à U1 pour obtenir la région
pour laquelle on a toujours ![]() dans [
dans [![]() ]
]
![]()
![]()
![]() Next:27.
Problèmes à résoudreUp:No
TitlePrevious:25.
Conception optimale
Next:27.
Problèmes à résoudreUp:No
TitlePrevious:25.
Conception optimale