Next:26. La conception optimaleUp:No TitlePrevious:24. État du projet

25. Conception optimale

détermination des dimensions d'un mécanisme pour avoir les performances optimales vis-à-vis d'un cahier des charges

25.1 Problème classique de théorie des mécanismes

Un exemple: le mécanisme à 4 barres
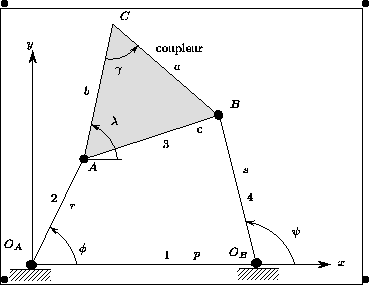
$\begin{picture}( 8.5, 6.5)( 1.189, 6.786)\put(1.189000,6.786000){$\bullet$ }\p......x$ }\put(5.02,9.99){3}\put(5.81,10.35){c}\put(6.60,10.93){$B$ }\end{picture}$ quand OA tourne le point C décrit une courbe algébrique

Deux théorèmes amusants en théorie des mécanismes:

$\bullet$ tout point d'un mécanisme à 1 d.d.l. constitué d'articulations rotoïdes décrit une courbe algébrique (Roth, 1967)

$\bullet$ réciproquement on peut toujours construire un mécanisme dont un point décrit une courbe algébrique donnée (Kempe, 1876)

La courbe suivie par le point C varie énormément selon les dimensions du mécanisme

$\begin{picture}( 11.3, 10.8)( 0.145, 3.480)\put(0.145000,3.480000){$\bullet$ }......in/./Mecanisme/divers-courbes-coupler.ps'' hscale=100 vscale=100}}\end{picture}$ Comment déterminer les dimensions d'un 4-barres pour obtenir une trajectoire voulue pour le point C ou s'en approcher ?

Cela revient à résoudre un système d'équations (une dizaine ou plus)

Next:26. La conception optimaleUp:No TitlePrevious:24. État du projet

Jean-Pierre Merlet

1999-11-16