Parallel processing
Parallelizing ALIAS programs
Interval analysis has a structure that is appropriate for a distributed implementation. Indeed the principle of the algorithm is to process a list of boxes, the processing for a box being independent of the other boxes in the list (except that it may have be stopped). A classical distributed implementation will rely on the master/slave paradigm. A master computer will manage the list of boxes and monitor the activity of the slaves. As soon as a slave is free the master will send a box to this slave. The slave, which has its own list of boxes, will perform a few iteration of the solving algorithm and then send back to the master the remaining boxes to be processed in its list and eventually the solutions it has found. After receiving a signal from the slave the master will receive the boxes from the slave and append them to its list of boxes. This slave being now free the master will send him another box in its list.
Hence most of the calculation will be performed by the slaves. It may happen however that at a given time all the slaves are busy processing boxes. The master itself may then start a few iteration of the solving algorithm on the current box of its list while carefully monitoring the activity of the slaves.
The structure of the interval analysis algorithms is very convenient for using the above paradigm:
- few data are to be transmitted by the master to the slave:
typically for a problem with
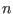 unknowns the master will have to send
2
unknowns the master will have to send
2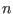 floating numbers that describe a box. It may however be
interesting to send other information such as the derivatives but
still the amount of data will be low
floating numbers that describe a box. It may however be
interesting to send other information such as the derivatives but
still the amount of data will be low
- the processing time of a box is in general much more large than the transmission time
The gain in computation time will in general be lower than the number of used slaves. This is due to
- the transmission time between the master and the slaves
- an overhead of the slave program: in our implementation the
slaves uses basically the same program than the master and perform
some coherence checks on the unknowns, equations, available memory
size
 before starting the processing of the box
before starting the processing of the box
- the fact that only one computer manages the list of boxes. This master may be still managing the boxes send by a slave while others slaves have already finished their processing. Clearly the master/slave paradigm exposed above may not be the best for a large number of computers. In a next version we intend to propose another paradigm for the use of the interval analysis algorithms in the framework of grid computing
In any case a key point of a distributed implementation is to be able to
- stop an algorithm that is run by a slave computer after it has performed some processing on a box
- recover the current state of the slave process i.e. the solutions if any and the remaining unprocessed boxes.
Stopping a procedure and miscellaneous utilities
There are different methods to stop the current bisection process:
- the number of boxes still to be processed
is greater than a given
threshold
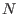 : this is obtained by setting the global variable
ALIAS_Parallel_Max_Bisection
to
: this is obtained by setting the global variable
ALIAS_Parallel_Max_Bisection
to 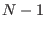 .
.
A safety procedure may be used as
the number of bisection may be large before getting the right number
of
boxes (for example when using the single bisection mode): the
maximal number of bisection may be indicated by setting the global
variable
ALIAS_Parallel_Max_Split
and the procedure will return if this
number is reached and the number of unprocessed boxes
is lower than ALIAS_Parallel_Max_Bisection (otherwise the
process will continue until this number is reached).
.
.
A safety procedure may be used as
the number of bisection may be large before getting the right number
of
boxes (for example when using the single bisection mode): the
maximal number of bisection may be indicated by setting the global
variable
ALIAS_Parallel_Max_Split
and the procedure will return if this
number is reached and the number of unprocessed boxes
is lower than ALIAS_Parallel_Max_Bisection (otherwise the
process will continue until this number is reached).
- the number of performed bisection is greater than a given
threshold
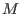 : this is obtained by setting the global variable
ALIAS_Parallel_Max_Bisection
to
: this is obtained by setting the global variable
ALIAS_Parallel_Max_Bisection
to 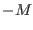
- the number of performed bisection is greater than a given
threshold
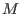 and the number of boxes still to be processed
is lower than a given
threshold
and the number of boxes still to be processed
is lower than a given
threshold 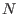 : this is obtained by setting the global variable
ALIAS_Parallel_Max_Bisection
to
: this is obtained by setting the global variable
ALIAS_Parallel_Max_Bisection
to 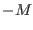 and the global variable
ALIAS_Parallel_Max_Box
to
and the global variable
ALIAS_Parallel_Max_Box
to 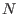 . A
safety mechanism is enforced in that case to avoid that only one of the
slave computer will perform all the computation: if
. A
safety mechanism is enforced in that case to avoid that only one of the
slave computer will perform all the computation: if 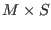 bisections have been done the procedure will return the error code
-1. The value of
bisections have been done the procedure will return the error code
-1. The value of 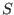 is given by the global variable
ALIAS_Safety_Factor with a default value of
2
is given by the global variable
ALIAS_Safety_Factor with a default value of
2
- if we are using the reverse storage mode we may indicate that
the number of performed bisection must be greater than a given
threshold
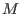 and the number of boxes still to be processed
is lower than a given
threshold
and the number of boxes still to be processed
is lower than a given
threshold 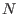 : this is obtained by setting the global variable
ALIAS_Parallel_Max_Bisection
to
: this is obtained by setting the global variable
ALIAS_Parallel_Max_Bisection
to 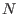 and the global variable
ALIAS_Parallel_Max_Reverse
to
and the global variable
ALIAS_Parallel_Max_Reverse
to 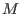
- the slave computation time has exceeded a fixed amount of time, which probably indicate that it will be preferable to distribute the treatment of the processed box among different slaves. This could be done using the double ALIAS_TimeOut which indicates the maximum amount of time (in minutes) during which a slave may run (this amount will be respected only approximatively).
ALIAS_Parallel_Box. Let ALIAS_Parallel_Box[0]=
Box_Solve_General_Interval(i,1)
Gradient_Solve_General_Interval while for the procedures involving the gradient and hessian of the functions the gradient may be retrieved in the interval matrix Gradient_Solve_JH_Interval. Note that this storage may not be available if you have set the flag ALIAS_Store_Gradient to 0 (its default value is 1).
The variable ALIAS_Parallel_Slave should be set to 0 for a sequential use of the algorithm, to 1 if the algorithm is run by a master computer and to 2 if the algorithm is run by a slave computer.
Using this stop criteria we may implement a parallel version of the ALIAS procedures, see the ALIAS-Maple manual.
If the master/slave scheme is used the master may perform some steps of a solving algorithm but for efficiency purpose it is necessary that the master monitor the slaves to determine if one has completed its calculation. This is the role of the ALIAS_Slave_Returned procedure that stops the processing done by the master as soon as a slave is free. Such a procedure may be found in the lib_Slave.a library: it is based on the pvm message passing mechanism (see the ALIAS-Maple manual). For the non parallel processing the equivalent procedure may be found in the lib_No_Slave.a library. Hence according to a sequential or a parallel use one of this library has to be linked to the main program.
For solving procedures involving the use of the gradient we may use two schemes:
- the master transmits to the slave both the boxes and the simplified gradient
- the master transmits to the slave only the boxes and the slave will first compute the simplified gradient before running the solving algorithm
The ALIAS-Maple library offers a parallel implementation of some solving algorithm. Communication between the slaves and the master is ensured by the message passing mechanism pvm. See the ALIAS-Maple manual for a detailed account of the distributed implementation.
This implementation uses some specific C++ procedures.
void ALIAS_Prepare_Buffer(int DimVar,INTERVAL_VECTOR &X,char *buffer)which put in the string buffer the lower and upper bounds of the DimVar ranges contained in the interval vector X.
The master and slaves exchange strings and in the parallel implementation offered currently by ALIAS all data are contained in these strings (this may change in the near future as PVM offers other possibility). Each numerical data is introduced by few control character. The following control character are used:
- B: the next floating point numbers will be a box that is sent back by the slave
- BS: same as B except that the box may be used as a parameter by the slave (for example the location of the current optimum)
- F: is followed by an integer. It's used by the slave to indicate how many solutions it will send to the master
- N: just used to indicate that a slave has completed its task and has nothing to send back to a slave
- P: followed by the control character I or F. Its allow to transmit to the slave an integer or a float that will be used as a parameter
- S: the next floating point numbers will be a solution box that is sent back by the slave
- SP: followed by an integer. It's used by the master to indicate to the slave the value of the parameter ALIAS_Parallel_Max_Bisection
Using this convention we may used the following procedure to decode the string sent by the master or the slave:
int ALIAS_Read_Buffer(char *mess,
int Nb_Var, int Nb_Eq,INTERVAL_MATRIX &Box,int *Nb_Total,
INTERVAL_MATRIX &Sol,int *Nb_Sol,int *Nb_Split,
INTEGER_VECTOR &IPar,int *Nb_Ipar,
VECTOR &FPar,int *Nb_Fpar,INTERVAL_MATRIX &BoxPar,
int *Nb_BoxPar)
where mess is the string and
- Box: the Nb_Total boxes with the control character B
- Sol: the Nb_Sol boxes with the control character S
- Nb_Split: the integer following F
- IPar: the Nb_Ipar integer following the control character P I
- FPar: the Nb_Fpar float following the control character P F
- BoxPar: the Nb_BoxPar parameter boxes following the control character BS
If is necessary we may transmit also the simplified jacobian associated to the boxes using the procedure:
int ALIAS_Read_Buffer_Gradient(char *mess,
int Nb_Var, int Nb_Eq,INTERVAL_MATRIX &Box,
INTEGER_MATRIX &GBox,int *Nb_Total,
INTERVAL_MATRIX &Sol,int *Nb_Sol,int *Nb_Split,
INTEGER_VECTOR &IPar,int *Nb_Ipar,
VECTOR &FPar,int *Nb_Fpar,INTERVAL_MATRIX &BoxPar,
int *Nb_BoxPar)
Here the boxes followed by the simplified jacobian GBox are introduced by the control character BG.
If the true jacobian has to be transmitted we use:
int ALIAS_Read_Buffer_Hessian(char *mess,
int Nb_Var, int Nb_Eq,INTERVAL_MATRIX &Box,
INTERVAL_MATRIX &GBox,int *Nb_Total,
INTERVAL_MATRIX &Sol,INTEGER_VECTOR &Is_Kanto,
int *Nb_Sol,int *Nb_Split,
INTEGER_VECTOR &IPar,int *Nb_Ipar,
VECTOR &FPar,int *Nb_Fpar,INTERVAL_MATRIX &BoxPar,
int *Nb_BoxPar)
Here the boxes followed by the jacobian GBox are
introduced by the control character BG.
Furthermore each solution is followed by an integer that indicates the
type of the solution and can be accessed by Is_Kanto.