


suivant: Perspectives
monter: Un meilleur filtrage
précédent: Mise en uvre
Table des matières
Avec Floyd-3B on obtient un filtrage très proche de la 3B-consistance.
L'instance pré-filtrée par cet algorithme peut alors être filtrée
plus efficacement par la 3B par rapport au problème initial,
puisque les domaines des variables ont été considérablement réduits.
Donc on a un filtrage supérieur ou égal à la 3B sur le problème initial.
Figure:
Une consistance globale pour l'exemple 3.1
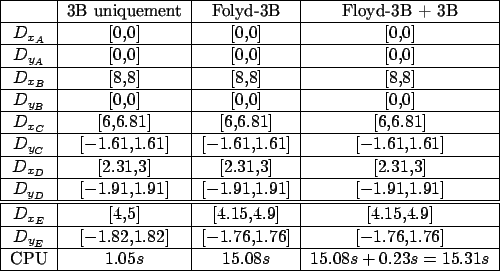 |
On peut constater cette amélioration du filtrage de
la 3B sur l'exemple 3.1. On avait dit qu'on ajoutait un point 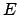 à l'exemple
1.1 au milieu de
à l'exemple
1.1 au milieu de 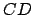 . Jusqu'à présent aucun des filtrages effectués
ne permettait d'obtenir les relations
. Jusqu'à présent aucun des filtrages effectués
ne permettait d'obtenir les relations
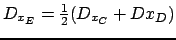 et
et
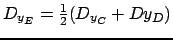 . Ici c'est chose faite puisque :
. Ici c'est chose faite puisque :
![$ \frac{1}{2}(D_{x_C} + D{x_D})=\frac{1}{2}([6,6.81] + [2.31,3]) = [4.15,4.9] = D_{x_E}$](img295.png)
![$ \frac{1}{2}(D_{y_C} + D{y_D})=\frac{1}{2}([-1.91,1.91] + [-1.61,1.61]) = [-1.76,1.76] = D_{y_E}$](img296.png)
Au niveau des performances, on ne peut pas comparer la 3B avec notre algorithme de fermeture-
filtrage.
Nous détaillons dans l'annexe, les résultats obtenus sur une instance à 12 points,
intitulé ``le problème des losanges'', et sur une instance à 15 points, le logo de l'école
des ponts. Sur ce dernier exemple, on obtient un gain en efficacité de l'ordre de 30%,
alors que sur l'exemple 3.1 les performances sont catastrophiques, mais pour
obtenir une consistance globale.



suivant: Perspectives
monter: Un meilleur filtrage
précédent: Mise en uvre
Table des matières
Heikel Batnini
2002-10-22

