Exemple 4.1
Soient 3 points
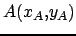
,
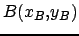
et
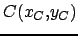
tels que :
Nos inconnues sont donc
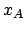
,
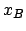
et
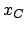
et les contraintes :
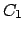
:
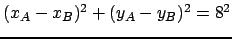
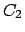
:
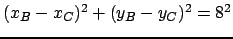
:
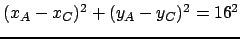
On remarque que
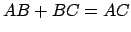
, ce qui veut dire que les 3 points sont alignés.
Ce système n'a pas de solutions puisqu'on ne peut pas aligner les 3 points
s'il sont instanciés dans leurs domaines.
Ici le
est 2B-consistant car les domaines vérifient localement toutes les contraintes,
pourtant le système n'a pas de solutions.
Voici l'instance
correspondante, on a :
-
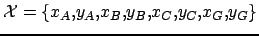 .
.
-
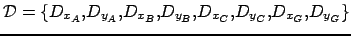 , avec :
, avec :
- Grâce aux formules de la propriété 4.1, on calcule les distances
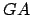 ,
, 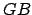 et
et 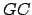 :
:
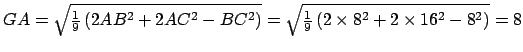
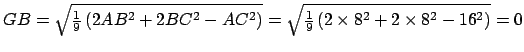
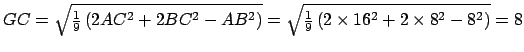
On ajoute aux contraintes ci-dessus, les contraintes suivantes :
 :
:
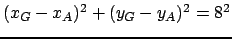
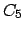 :
:
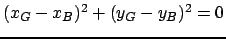
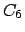 :
:
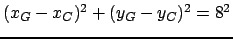
Lorsqu'on veut résoudre cette instance par la 2B, on a la réponse immédiatement puisque
la contrainte
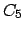
est violée.
En effet, elle signifie que les points
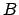
et
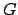
sont confondus,
or leurs domaines en
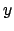
ont une intersection vide.
On peut donc remplacer la procedure FILTER-DOMAINS par une
méthode qui calcule les données de l'instance 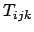 , puis
la résout par 3B, avec effets de bord sur l'instance du problème initial.
On appelle cette procédure Floyd-3B :
, puis
la résout par 3B, avec effets de bord sur l'instance du problème initial.
On appelle cette procédure Floyd-3B :
procedure Floyd-3B(
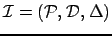 )
)
pour k
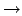 1 à
1 à 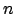 faire
faire
pour j
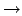 1 à
1 à 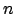 faire
faire
pour i
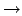 1 à
1 à 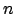 faire
faire
si
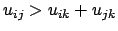 alors
alors
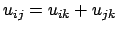
si
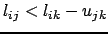 alors
alors
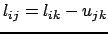
sinon si
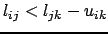 alors
alors
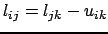
si
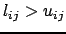 alors Erreur
alors Erreur
3B(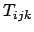 )
)
finpour
finpour
finpour
retourner
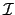
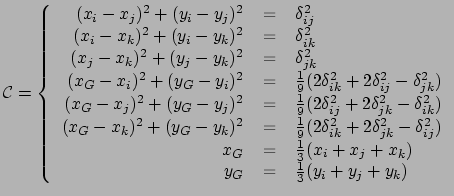
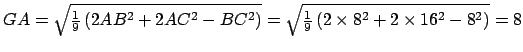
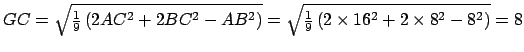
![]() , puis
la résout par 3B, avec effets de bord sur l'instance du problème initial.
On appelle cette procédure Floyd-3B :
, puis
la résout par 3B, avec effets de bord sur l'instance du problème initial.
On appelle cette procédure Floyd-3B :
![]() )
)
![]() 1 à
1 à ![]() faire
faire
![]() 1 à
1 à ![]() faire
faire
![]() 1 à
1 à ![]() faire
faire
![]() alors
alors
![]()
![]() alors
alors
![]()
![]() alors
alors
![]()
![]() alors Erreur
alors Erreur
![]() )
)
![]()