Filtrage d'une instance complète

Supposons que l'instance $\mathcal{I}=(\mathcal{P},\:\mathcal{D},\:\Delta)$ soit transformée, comme on l'a vu dans la section précédente, en une instance complète $\mathcal{I}_f$. On peut lui appliquer les méthodes de filtrage local Les performances de ces algorithmes dépendent de $A$, la taille maximale des domaines des variables c'est-à-dire le nombre de flottants du plus grand domaine. La taille des intervalles, en particulier des domaines des distances, ne peut être que réduite par l'algorithme de fermeture, ce qui implique une amélioration des performances de ces méthodes.

Figure: Fermeture du graphe de distance associé à l'exemple 3.1

En revanche, si les données du problème sont trop larges les performances peuvent être dégradées, la fermeture du graphe ajoutant plusieurs contraintes par rapport au problème initial. On peut cependant espérer un gain de temps considérable dans la plupart des cas. Considérons l'exemple qui suit :

Exemple 3.1   Reprenons l'exemple du quadrilatère $ABCD$ (exemple 1.1), en y ajoutant un nouveau point $E$ au milieu de $[CD]$ :

$A(0,0)$, $B(8,0)$, $C(x_C,y_C)$, $D(x_D,y_D)$ $E(x_E,y_E)$
$AB=8$, $AD=3$, $BC=2$, $CD=4$ $CE=2$ $DE=2$
$D_{x_C}=[6,10]$, $D_{y_C}=[-2,2]$
$D_{x_D}=[-3,3]$, $D_{y_D}=[-3,3]$
$D_{x_E}=[-20,20]$, $D_{y_E}=[-20,20]$

Ce qui nous conduit à poser le système sous-contraint :

$C_1$ : ${(x_C - 8)}^2 + {y_C}^2 = 4$

$C_2$ : ${(x_D - x_C)}^2 + {(y_D - y_C)}^2 = 16$

$C_3$ : ${(x_E - x_C)}^2 + {(y_E - y_C)}^2 = 4$

$C_4$ : ${(x_D - x_E)}^2 + {(y_D - y_E)}^2 = 4$

$C_5$ : ${x_D}^2 + {y_D}^2 = 9$

Le graphe de distance complété, comme l'illustre la figure 5, ajoute des informations dont on ne disposait pas initialement dans la formulation du problème, mais qui sont induites par les propriétés géomètriques du système. Ces informations sont d'autant plus intéressantes qu'elles sont relatives à l'ensemble des points, et non à un couple de points, comme les distances données. Par exemple, la longueur du segment $AC$ est nécessairement inférieure à $AD+CD=7$ et supérieure à $AB-BC=6$ pour que les triangles $ACD$ et $ABC$ existent, ce qui ne contredit pas l'existence du triangle $ACE$. $AC$ est donc contraint d'appartenir à l'intervalle [6,7], qui est calculé en utilisant tous les autres points du graphe.

Figure: Comparatifs des résultats de la 3B et de la 2B pour l'instance $I$ de l'exemple 3.1 et pour $I_f$, fermeture de $I$.

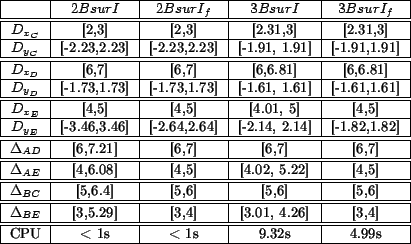
Pour cet exemple, nous avons utilisé la 2B pour résoudre INEQ( $\mathcal{I}$). En utilisant l'instance fermée on a un gain de temps de calcul de l'ordre de 50% pour la 3B (voir figure 6). Les tests ont été effectués sur un Pentium II 233Mhz avec 64Mo de RAM, avec prolog IV pour la 2B et Ilog Solver pour la 3B. Les même tests ont été effectués sur un problème à 15 points, le logo de l'école des ponts, avec un gain de temps de l'ordre 90% pour la 3B (les résultats détaillés sont dans l' annexe).

On peut voir également sur ce tableau, que les résultats de la 2B et de la 3B sont plus précis. Le point $E$, celui qui est le plus éloigné des points fixés $A$ et $B$, bénéficie d'un raffinement conséquent sur le domaine de ses coordonnées, notemment pour $y_E$. Ces résultats s'expliquent par le fait que la propagation d'intervalles entre 2 points du graphe se fait instantanément et avec moins de pertes puisque la liaison entre ces 2 points est directe. Comme on l'a vu dans la section 2.3, la 2B perd du temps et de la précision à propager localement une information d'un bout à l'autre du graphe, de contraintes en contraintes. Ici, le filtrage local entre 2 points du graphe se fait en traitant une seule et unique contrainte. Enfin l'intègrité de l'espace des solutions est respectée, puisque les solutions de l'instance initiale vérifient les inégalités triangulaires et sont donc solutions de l'instance fermée.