Définitions et propriétés

Définition 4.1 (Centre de gravité d'un triangle(en dimension 2))   Soit $ABC$ un triangle, tel que $A(x_A,y_A)$, $B(x_B,y_B)$ et $C(x_C,y_C)$. Le centre de gravité $G$ du triangle $ABC$ est défini par l'égalité vectorielle $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{O}$. On a alors :

• $x_G = \frac{x_A + x_B + x_C}{3}$
• $y_G = \frac{y_A + y_B + y_C}{3}$

La proposition suivante, dont la preuve est en annexe, est un corollaire de la proposition 5.2 pour $n=3$. Elle nous donne une relation forte entre les distances entre le centre de gravité d'un triangle et un sommet de ses sommets.

Propriété 4.1   Soit $ABC$ un triangle non dégénéré (et $G$ son centre de gravité. Alors on a les égalités suivantes :

• $GA^2=\frac{1}{9}(2AB^2+2AC^2-BC^2)$
• $GB^2=\frac{1}{9}(2AB^2+2BC^2-AC^2)$
• $GC^2=\frac{1}{9}(2AC^2+2BC^2-AB^2)$

Remarque   Les domaines des distances entre deux sommets d'un triangle quelconque d'une instance fermée par l'algorithme de fermeture-filtrage, vérifient les inégalités triangulaires. Dans ce cas, les parties gauches des égalités ci-dessus sont toujours des intervalles dont les bornes sont positives ou nulles. En effet d'après les inégalités triangulaires on a :
$0 \leq \vert AB-AC\vert \leq BC \leq AB+AC$
$\Rightarrow \vert AB-AC\vert^2 \leq BC^2 \leq (AB+AC)^2$
$\Leftrightarrow AB^2+AC^2-2.AB.AC \leq BC^2 \leq AB^2+AC^2+2.AB.AC$
$\Leftrightarrow -(AB^2+AC^2)-2.AB.AC \leq -(2AB^2 + 2AC^2)+BC^2 \leq -(AB^2+AC^2)+2.AB.AC$
$\Leftrightarrow \frac{1}{9}(AB-AC)^2 \leq GA^2 \leq \frac{1}{9}(AB+AC)^2$
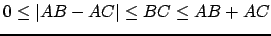
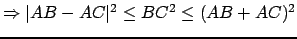
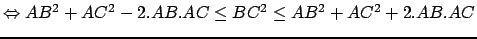
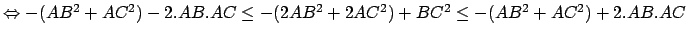
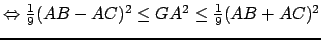
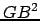
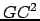
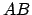
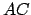
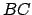
On peut évidemment trouver le même type d'encadrement pour $GB^2$ et $GC^2$. Cela permet d'affirmer que les domaines des distances entre un sommet quelconque d'un triangle et le centre de gravité de ce triangle sont calculables en utilisant l'arithmétique des intervalles. On est toujours dépendant de la précision des domaines des distances $AB$, $AC$ et $BC$. 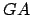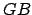Des domaines trop larges pour ces distances, nous donnerait un encadrement trop large des distances $GA$, $GB$, et $GC$. 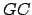Malgré tout elles nous permettrons quand même d'avoir un filtrage au moins équivalent à ce que l'on pourrait faire sans le centre de gravité.