Many problems in scientific computation and in applications such as CAGD, robotics, computer vision, molecular biology, signal processing... involves algebra and geometry. The objective of the project is to develop algorithmic methods for effective and reliable resolution of these geometric and algebraic problems.
Our research in effective algebraic geometry includes methods to solve polynomial equations, to compute resultants, to factorise polynomials, to detect and analyse singularities of algebraic varieties, to describe the topology of semi-algebraic sets. We are specially interested in problems on semi-algebraic curves and surfaces, such as intersection, singularity, topology, arrangement computations. These geometric investigations lead to algebraic questions, and particularly to the resolution of polynomial equations. We work on the design and analysis of new methods based for instance on normal form computation, resultants or subdivision techniques.
|
 |
 |
Approximate numerical calculations, is usually opposed to symbolic calculations. We are exploring these bonds between geometry, algebra and numerical computation. How to deal with approximate semi-algebraic models ? How to control the error and to certify the results in numerical algebraic geometry computation ? How to improve the representation of our problem ? These are investigations we are following, in this emmerging field at the frontier between symbolic and numeric computation.
|
The implementation and validation of our algorithms form another important component of our activity. We pay attention to problems of genericity, modularity, effectiveness, suitable for the writing of algebraic and geometrical codes. We develop the following software:
-
packages for the open-source project mathemagix (polynomial solvers, algebraic-geometric computation, ...).
-
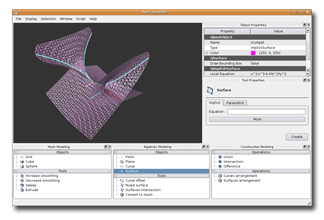
Axel, an algebraic-geometric modeler.
-
Multires, a maple package for resultant and residu computation.
|
|
|