Reactive approach in simulation and modeling of physical systems
Many interesting systems in physics consist of linked entities. Continuous system dynamics can be described by, possibly large, systems of differential equations. Here we consider the ordinary differential equations. Often a system does not have an exact analytical solution (non-linear differential equations) so a numerical solution is the best available. Two main phases are : discretization of time and then integration using, for example, some stepwise methods (iterative algorithms).
Notwithstanding simulation of pure continuous and pure discrete systems is well-understood, the building of initial models and their numerical resolution can become very complicated, especially when modeling of mixed continuous/discret behavior (hybrid phenomena) is needed.
Here we present some examples of application of the
reactive approach in modeling and simulation of continuous (and hybrid) phenomena. This technique gives a very simple and modular way to describe the evolution of complex physical models. The main features of this approach are simplicity of model construction and high modularity of components. This approach allows to express both continuous and discret aspects of a model.
The aim of the reactive approach is to propose a structured and flexible paradigm for programming dynamic reactive systems. A reactive system is composed of a set of synchronously executed parallel components communicating by instataneous broadcast events (communication is similar to the radio transmission where emitters send information that is instantaneously received by all listeners). The model proceeds in successive reactions, one at each logical instant. At each instant, the reaction is computed using the current tuple of input events and some internal information. The global behavior of such a system results from the cooperation of its components (subsystems).
A reactive program plays the role of an independent logical process describing a behavior of an entity and operating on its associated state (which can be incapsulated in an appropriate logical object). Implementations exist on
C and Java and provide a set of basic primitives (sequential and parallel execution, preemption, reaction on events, loops, conditions) with clear and precise semantic rules. Reactive machines execute the reactive instructions and allow to dynamically add and remove (to preempt) the components and theirs programs from the environment of execution.A reactive object is an object containing the state variables plus associated reactive program that implements its behavior.
Using the synchronous execution, a complex system can be represented as a set of linked but independent entities with a common discret time (instants). Linkage translates into events (for example, forces between particles), thus the model is very modular : adding new receivers to the system is totally transparent and does not affect the functionality of the other components.
We can adapt many of the numerical algorithms of integration that are in standard use by mapping theirs steps onto the logical instants. Thus, one can simulate a complex physical system in very natural way by simply putting many reactive objects in parallel, that means that we have many parallel synchronized processes of integration communicating by broadcast events. Each process can be controled and preempted as well as new components can be dynamically added in the system without any global reinitialization.
Let's bring a simple example of the implementation of the principles mentioned above. The first image shows general block-function diagram of any component. Central block corresponds to a system of differential equations (for example, coupled equations for newtonian motion). The input entries are received events and the output events (g vector) are some functions depending on the value of the state vector (let's call them influences). Input and output entries of all the components are synchronized in a natural way.
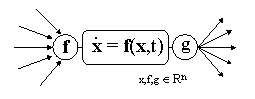
The second image is a possible general schemes of reactive program of components corresponding to one step of calculation (the body of the main loop). It can be composed of three main parts : emission of influences, reception and collection of external influences and computation of the next state (or of a next estimation) using some of the simpler numerical methods (we use Euler, Verlet and Runge-Kutta4 methods). This program is self-starting.
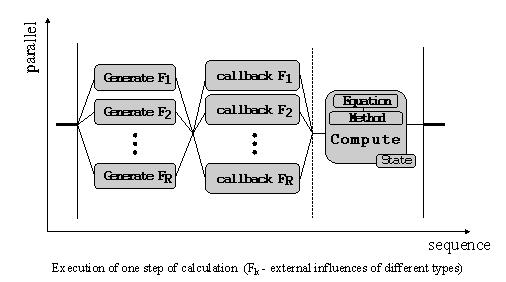
Note that this scheme offers a natural way to build a behavior of an object just by putting appropriate elementary blocks (behaviors) in parallel. This facility can be employed, for example, in educational process
The
Icobj package provides two powerfull mechanisms : visual representation of reactive objects and dynamical graphical construction of theirs behaviors from basic elementary behaviors (as "move right", "move up", "attract", "bounce", etc). One can consider this package (with some extensions) as a low-level block diagram simulator.Here you can find some examples of use of this approach (based on a simple web-version of Icobj framework). There are only some predefined ready-to-use configurations, however you can construct your own simulations with web-version (soon available here).
Examples (best viewed with Internet Explorer for Windows and Netscape Navigator for Unix)
You can see also
this paper (a DEA stage report, in French) containing more detailed description of this technique as well as its first implementation on Java.
Please,
mail for any comments and suggestions.
2002-07-18