Symmetric tensors

using PolyExp

We consider symmetric tensors or equivalently homogeneous polynomials, in the following variables:

x = @ring x0 x1 x2;

A symmetric tensor of order d=4 and of rank 3.

d=4; t = (x0+x1+0.75x2)^d + 1.5*(x0-x1)^d -2.0*(x0-x2)^d

0.5x0^4 - 2.0x0^3x1 + 11.0x0^3x2 + 15.0x0^2x1^2 + 9.0x0^2x1x2 - 8.625x0^2x2^2 - 2.0x0x1^3 + 9.0x0x1^2x2 + 6.75x0x1x2^2 + 9.6875x0x2^3 + 2.5x1^4 + 3.0x1^3x2 + 3.375x1^2x2^2 + 1.6875x1x2^3 - 1.68359375x2^4

The graph of the homogeneous polynomial $(x0+x1+0.75x2)^4 + 1.5(x0-x1)^4 -2(x0-x2)^4$ in polar coordinates on the sphere looks like this:

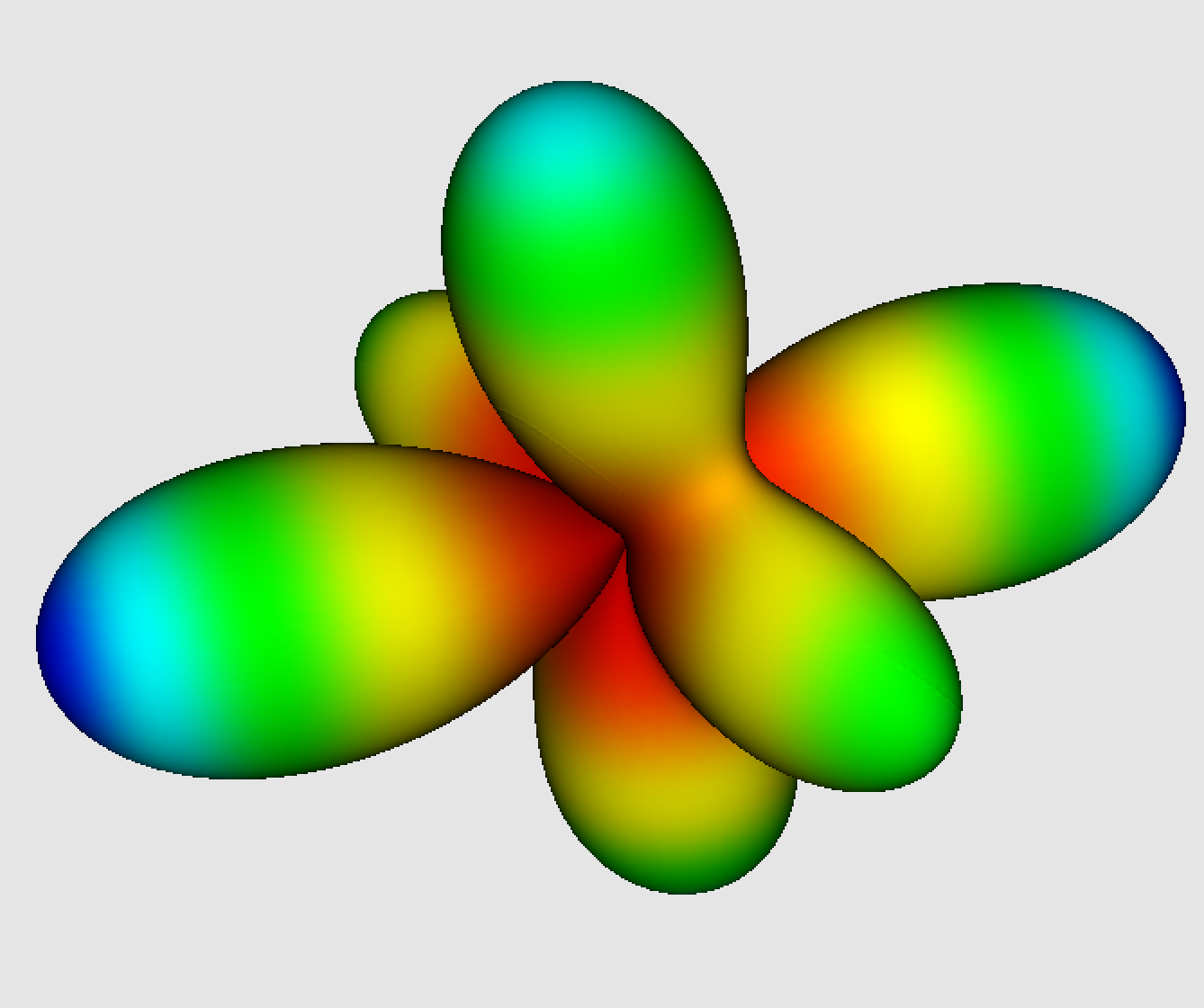
We associate to $t$, the following (truncated) series in the dual variables, after substituting $x0$ by 1:

s = series(t, x0, d)

0.5 + 0.421875dx1*dx2^3 + 0.5625dx1^2dx2^2 + 0.75dx1*dx2 + 0.75dx1^3dx2 - 0.5dx1^3 + 0.75dx1^2dx2 + 2.421875dx2^3 + 2.5dx1^4 + 2.75dx2 - 1.68359375dx2^4 + 0.5625dx1*dx2^2 - 0.5dx1 + 2.5dx1^2 - 1.4375dx2^2

Computing its decomposition

w, Xi = svd_decompose(s);

yields the weights w

w

3-element Array{Float64,1}:
  1.0
 -2.0
  1.5

and the corresponding points Xi, which are the coefficients of x1, x2 in the linear forms of the decomposition of the tensor t:

Xi

3×2 Array{Float64,2}:
  1.0           0.75      
  7.51046e-16  -1.0       
 -1.0           1.1339e-15