Multivariate exponential decompositon

Multivariate exponential decompositon

using PolyExp

We consider the following function, which is a sum of 6 complex exponentials 

f = (u,v) -> 0.5*cos(0.7*pi*(u+v))+0.6*sin(4*pi*u)-0.2*cos(pi*v);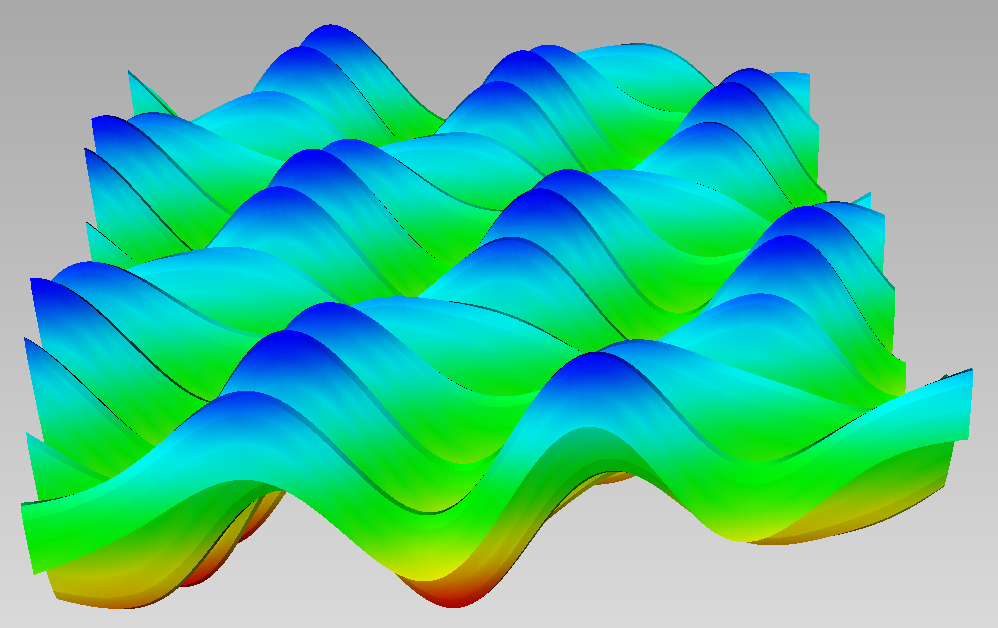

waves

In order to recover the frequencies or exponents of these exponential terms and their coefficients, we sample the function on a grid $({\alpha_1 \over T}, {\alpha_2 \over T}), \alpha=(\alpha_1,\alpha_2)\in A\subset \mathbb{N}^2$. This defines a sequence of moments $\sigma_{\alpha}=f({\alpha_1 \over T}, {\alpha_2 \over T})$. We compute its generating series truncated in degree $\leq 5$.

x = @ring x1 x2
L = monoms(x,5)
T = 10
mnt = (V->f(V[1]/T,V[2]/T))
sigma = series(mnt, L)
0.5095797473748392dx1^2dx2^2 - 0.4519219149027473dx1^4 + 0.6050846776084937dx1^2 + 0.46210935078676274dx1^2dx2^3 + 0.2775204557293506dx2^3 + 0.8328361327510712dx1*dx2 + 0.2569085959993554dx2^4 + 0.5575373543042985dx1^2dx2 - 0.5338499631663495dx1^4dx2 - 0.2874793003806999dx1^3dx2^2 - 0.15759364518763863dx1^3 + 0.7717888541929423dx1*dx2^3 + 0.02699524986977328dx1^5 + 0.7358257607718759dx1*dx2^4 - 0.22417045976016967dx1^3dx2 + 0.22699524986977343dx2^5 + 0.8585922907464658dx1 + 0.29774707771034303dx2 + 0.2906101273580203dx2^2 + 0.8039080170899477dx1*dx2^2 + 0.3

Computing its decomposition using svd

w, Xi = svd_decompose(sigma);

yields the weights w of the exponential terms in f and the exponentials Xi:

w
6-element Array{Complex{Float64},1}:
 5.11396e-14-0.3im        
 5.08482e-14+0.3im        
        0.25+9.12936e-13im
        0.25-9.12867e-13im
        -0.1-9.83498e-13im
        -0.1+9.83474e-13im

By taking the log and scaling by ${T\over \pi}$, we recover the frequency vectors within precision 1O^{-11}. 

log.(Xi)*T/pi
6×2 Array{Complex{Float64},2}:
  1.74732e-13+4.0im           -2.8625e-14+4.82382e-14im
  1.74732e-13-4.0im           -2.8625e-14-4.82382e-14im
  2.94123e-12+0.7im          -9.31825e-13+0.7im        
  2.94123e-12-0.7im          -9.31825e-13-0.7im        
 -1.27717e-12-1.00136e-11im   1.23403e-12+1.0im        
 -1.27717e-12+1.00136e-11im   1.23403e-12-1.0im