

suivant: L'approche de commande par
monter: INRIA
précédent: INRIA
Commande d'un manipulateur mobile non-holonôme
(M. Fruchard, doctorant, P. Morin, C. Samson)
Au cours de la première année du projet, nous avions traité le cas réputé plus simple d'un manipulateur mobile redondant et holonôme en utilisant le
formalisme de l'approche de commande par fonctions de tâches [#!Oxford91!#]. Ce formalisme fournit un cadre méthodologique général
pour la commande des systèmes robotiques holonômes. Nous l'avons repris
pour l'adapter au problème de suivi d'un objet par un manipulateur mobile redondant dont la base est omnidirectionnelle. Les lois
de commande que nous avons synthétisées de cette façon ont été validées
par des simulations sous MATLAB.
Forts de cette expérience, nous avons abordé cette année le cas d'un
manipulateur mobile dont la base est sujette à des contraintes non-holonômes.
La difficulté à commander les systèmes non-holonômes est essentiellement liée
au fait que les approximations linéaires de ces systèmes, en un point
d'équilibre, ne sont pas stabilisables.
L'approche par fonctions transverses [#!morin01-siam!#],
[#!morin03-jesa!#], [#!morin03-tac!#] que nous développons depuis quelques années est une alternative
à d'autres approches de synthèse de lois de commande par retour d'état
pour la stabilisation de ces systèmes. Une des pierres angulaires de
l'approche est qu'elle vise en premier lieu à assurer la stabilisation
asymptotique, non pas
d'un point d'équilibre du système, mais d'un ensemble contenu dans voisinage
arbitrairement petit de ce point (voir Fig. ![[*]](crossref.png) ). Il s'agit
donc d'une forme de stabilisation pratique. Pour préciser un
peu les choses sur le plan technique, considérons un système non-holonôme
commandable dont le mouvement est régi par une équation de la forme:
). Il s'agit
donc d'une forme de stabilisation pratique. Pour préciser un
peu les choses sur le plan technique, considérons un système non-holonôme
commandable dont le mouvement est régi par une équation de la forme:
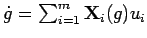 , avec
, avec  et
et
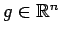 l'état
du système. Supposons, pour simplifier, que ce système possède une approximation homogène commandable dont les champs de commande engendrent une algèbre de
Lie de dimension
l'état
du système. Supposons, pour simplifier, que ce système possède une approximation homogène commandable dont les champs de commande engendrent une algèbre de
Lie de dimension 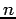 . L'approche par fonctions transverses repose sur l'existence (démontrée) d'une fonction
. L'approche par fonctions transverses repose sur l'existence (démontrée) d'une fonction 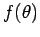 ,
,  appartenant au tore de dimension
appartenant au tore de dimension  , périodique et bornée dont la variation
infinitésimale, en un point
, périodique et bornée dont la variation
infinitésimale, en un point  quelconque, est "transverse" aux
directions données par les champs de vecteurs
quelconque, est "transverse" aux
directions données par les champs de vecteurs 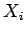 évalués en
évalués en
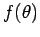 . Cette fonction peut d'autre part être associée à un
changement de variables
. Cette fonction peut d'autre part être associée à un
changement de variables
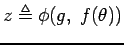 ,
,
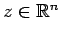 , tel que
, tel que 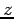 est d'autant plus proche de
est d'autant plus proche de 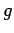 que
que
 est petit, et tel que, le long des trajectoires du système, la variation de
est petit, et tel que, le long des trajectoires du système, la variation de 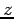 est donnée par:
est donnée par:
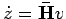 , avec
, avec
 inversible (grâce à la propriété de transversalité évoquée ci-dessus) et
inversible (grâce à la propriété de transversalité évoquée ci-dessus) et
![$ v = [u_1,\cdots,u_m,\dot{\theta}_1,\cdots,\dot{\theta}_{n-m}]^t$](img16.png) . En interprétant
. En interprétant 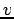 comme un vecteur de
commande de dimension
comme un vecteur de
commande de dimension 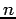 , l'équation de variation de
, l'équation de variation de 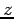 est formellement
similaire à
celle d'un système holonôme complètement commandé, disposant d'autant de variables de commande (ou de degrés de liberté) que de variables à commander.
L'application de l'approche par fonctions transverses revient donc, d'une
certaine manière, à ``substituer'' au système non-holonôme de départ, dont l'état est
est formellement
similaire à
celle d'un système holonôme complètement commandé, disposant d'autant de variables de commande (ou de degrés de liberté) que de variables à commander.
L'application de l'approche par fonctions transverses revient donc, d'une
certaine manière, à ``substituer'' au système non-holonôme de départ, dont l'état est 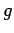 , un système ``voisin'' holonôme, dont l'état est
, un système ``voisin'' holonôme, dont l'état est 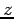 .
.
Figure:
Base mobile de type unicycle (au centre), sa transformée
omnidirectionnelle (cerclée), et la projection sur le plan de l'ensemble
image de la fonction transverse utilisée pour la transformation (en noir).
|
|
Une des applications immédiate de cette approche est la stabilisation
pratique d'une trajectoire de référence quelconque, c.a.d. non
nécessairement réalisable par le système non-holonôme. La méthode a été
validée en
simulation et expérimentalement sur notre robot mobile de laboratoire
ANIS, dans le cadre du suivi référencé vision d'une cible omnidirectionnelle
par un véhicule de type unicycle [#!artus03!#].
Son adaptation à la
manipulation mobile n'est cependant pas directe, parce qu'il importe,
complémentairement à l'objectif de stabilisation pratique,
de respecter les contraintes ``fortes'' associées aux objectifs de
manipulation au niveau de l'organe terminal du manipulateur. Cette difficulté,
et le souci de faciliter conceptuellement le couplage avec
l'approche par fonctions de tâches utilisée pour les manipulateurs mobiles
holonômes --ou avec toute autre méthodologie de synthèse de commande de
manipulateurs holonômes--, nous ont conduits à introduire la notion de
manipulateur
mobile omnidirectionnel équivalent au système non-holonôme,
pour la tâche de manipulation considérée. La notion d'équivalence repose ici
sur l'existence
d'un changement de coordonnées i) faisant passer de l'état du système
non-holonôme à l'état ``voisin'' (au sens de l'approche par fonctions
transverses) d'un système omnidirectionnel virtuel, et ii) laissant
invariantes certaines équations de contraintes de sorte que la réalisation de
l'objectif de manipulation, au niveau de l'effecteur, pour un des systèmes
entraîne la réalisation de cet objectif pour le second (voir Fig. ![[*]](crossref.png) ). L'existence d'un tel changement de variables est liée à la redondance mécanique du système. Le problème, tel que posé ci-dessus, admet aussi
plusieurs solutions du fait que plusieurs jeux de contraintes sont
envisageables. La détermination d'une solution ``meilleure'' que les autres
demeure, pour l'instant, une question ouverte.
). L'existence d'un tel changement de variables est liée à la redondance mécanique du système. Le problème, tel que posé ci-dessus, admet aussi
plusieurs solutions du fait que plusieurs jeux de contraintes sont
envisageables. La détermination d'une solution ``meilleure'' que les autres
demeure, pour l'instant, une question ouverte.
Figure:
Manipulateur mobile non-holonôme et le manipulateur mobile
omnidirectionnel équivalent, pour une tâche de suivi de cible.
|
|
L'intérêt de définir un manipulateur mobile omnidirectionnel équivalent
est de permettre de ramener le problème de synthèse de commande à
celui, plus simple, du cas holonôme étudié précédemment. En particulier,
l'application de l'approche par fonctions de
tâches à ce système virtuel permet de déterminer une loi de commande
cinématique pour ce système. Il ne reste plus alors qu'à utiliser les relations
(biunivoques, grâce aux propriétés de transversalité de la fonction
intervenant dans le changement de coordonnées) entre les entrées des
deux systèmes pour obtenir la loi
de commande équivalente pour le système physique non-holonôme.
Cette méthode a été testée en simulation pour un manipulateur mobile dont la
base
non-holonôme est de type unicycle, dans le cadre d'un problème de suivi de cible référencé vision.
La suite de ce travail portera sur:
- Le traitement d'un certain nombre d'aspects techniques liés à la mise en
 uvre des commandes sur un système physique.
uvre des commandes sur un système physique.
- L'implémentation et l'expérimentation sur notre manipulateur mobile
ANIS.
- La généralisation de la méthode à des architectures robotiques différentes (robots mobiles à bases non-holonômes de type voiture, par exemple), et pour la réalisation d'autres tâches robotiques.


suivant: L'approche de commande par
monter: INRIA
précédent: INRIA
Matthieu Fruchard
2003-10-01
![\includegraphics[width=0.65\textwidth]{images/fepsilon4.eps}](img18.png)
![[*]](crossref.png) ). Il s'agit
donc d'une forme de stabilisation pratique. Pour préciser un
peu les choses sur le plan technique, considérons un système non-holonôme
commandable dont le mouvement est régi par une équation de la forme:
). Il s'agit
donc d'une forme de stabilisation pratique. Pour préciser un
peu les choses sur le plan technique, considérons un système non-holonôme
commandable dont le mouvement est régi par une équation de la forme:
![\includegraphics[width=0.65\textwidth]{images/fepsilon4.eps}](img18.png)
![[*]](crossref.png) ). L'existence d'un tel changement de variables est liée à la redondance mécanique du système. Le problème, tel que posé ci-dessus, admet aussi
plusieurs solutions du fait que plusieurs jeux de contraintes sont
envisageables. La détermination d'une solution ``meilleure'' que les autres
demeure, pour l'instant, une question ouverte.
). L'existence d'un tel changement de variables est liée à la redondance mécanique du système. Le problème, tel que posé ci-dessus, admet aussi
plusieurs solutions du fait que plusieurs jeux de contraintes sont
envisageables. La détermination d'une solution ``meilleure'' que les autres
demeure, pour l'instant, une question ouverte.
![\includegraphics[width=0.65\textwidth]{images/STE_RP3.eps}](img19.png)