- Equations, Gradient and Hessian
- MakeF, MakeJ, MakeH
- Improving the efficiency of the code
- Function involving determinants
- Dealing with undefined expressions
- Interval valuation and the Problem_Expression package
- Interval evaluation of an expression in Maple
- Generating code
Interval evaluation in ALIAS-Maple
Clearly for any interval analysis method that deal with a problem involving expressions it is necessary to have a program that is able to interval evaluate these expressions. We will see also that having a program to interval evaluate the first and second derivatives may help to solve the problem. ALIAS-Maple provides various procedures that allow to create automatically such C++ program, being given only the expressions in Maple. These procedures will be presented in the next section. For testing purposes it may be interesting to have in Maple a procedure that interval evaluate an expression: such procedure will be presented in section 2.2. Special C++ code generating procedures will be presented in the section 2.3.
Equations, Gradient and Hessian
MakeF, MakeJ, MakeH
This set of procedures enable one to generate automatically C++ code for later use with the ALIAS-C++ library:
- MakeF: generates the procedure for evaluating a set of equations. These equations may be composed of most classical mathematical functions (see section 3.1.1 for a list of allowed operators) but may also include unexpanded determinants (see section 2.1.3).
- MakeJ: generates the procedure for evaluating the gradient of a set of equations
- MakeH: generates the procedure for evaluating the Hessian of a set of equations
Make[FJH]("[C++ file name]","[procedure name]",[list of equations],[list of unknowns]);
Thus:
with(ALIAS):
expr := [x^2+y^2-1,x+y]:
MakeF("Test.C","Test",expr,[x,y]);
enable to create the following C++ program Test.C
/* Code automatically written by Maple */
INTERVAL_VECTOR Test(int l1, int l2, INTERVAL_VECTOR & v_IS) {
INTERVAL_VECTOR V(2);
if (l1<=1 && 1<=l2)
V(1)=Sqr(v_IS(1))+Sqr(v_IS(2))-1;
if (l1<=2 && 2<=l2)
V(2)=v_IS(1)+v_IS(2);
return V;
}
Note that the program generated by MakeF has a specific form
that allows to interval evaluate all expressions or a specific set of
expressions: such format will be called the MakeF format. There
are also a MakeJ and MakeH format.
The procedures Make[FJH] makes an extensive use of the procedure
MinimalCout that try to find the optimal formulation of an
expression with respect to interval arithmetic. Indeed not all
mathematically equivalent formulation of an expression are interval
equivalent (i.e. they produce the same interval evaluation). For
example ![]() and
and ![]() are equivalent but the second
formulation always produces the optimal interval evaluation as there
is only one occurrence of
are equivalent but the second
formulation always produces the optimal interval evaluation as there
is only one occurrence of ![]() . For further detail on
MinimalCout see
section 9.7. Note that the variable
`ALIAS/mincout` plays
an important role in the calculation time of these procedures.
. For further detail on
MinimalCout see
section 9.7. Note that the variable
`ALIAS/mincout` plays
an important role in the calculation time of these procedures.
Note that not all expression can be interval evaluated (e.g. 1/x cannot be evaluated if the interval for x includes 0). ALIAS provide an automatic way to avoid evaluation problems (see section 2.1.5). If you use your own procedure and are aware of evaluation problems and modify the returned values it will be a good policy to set C++ flags ALIAS_ChangeF, ALIAS_ChangeJ to 1 (default value 0) if a change occurs: this will allow the ALIAS C++ library to avoid using improperly the returned value (e.g in the interval Newton scheme).
There are two "optimized" versions of MakeF and MakeJ called MakeFO and MakeJO that may produce a better code from the view point of interval evaluation but with a larger computation time. Note that the Code procedure may be used to produce simple C++ equivalent of a formula. Note also that inequalities are also recognized by these procedures.
In most of the ALIAS-Maple procedures it may be possible for the user to provide its own procedure for the evaluation of the expressions and of their derivatives. This is obtained by setting the flag `ALIAS/user_func` to a string that is the name of the C++ file that defines a procedure which will be used for evaluating the expressions (the name of the procedure must be F. Similarly the flag `ALIAS/user_derivative` may be used for the derivative of the expressions in which the procedure name must be J.
For the MakeF the end-user may also indicate that he has already written the expressions in a form that is optimal and that MakeF should only translate as it the expression in C++ without any modification by setting the flag `ALIAS/as_itF` to 1.
For the MakeJ procedure the end-user may also indicate that he has already computed the derivatives by setting the flag `ALIAS/as_itJ` to 1 and by defining the variable `ALIAS/as_itJ_array` as an array that contains the derivatives of all the expressions (the i-th row of this array contains the derivatives of the i-th expression with respect to the variables). If you have determinant in the expression you have to set the flag `ALIAS/as_itJ_mat` to 1 to avoid MakeJ trying to find a better evaluation function.
Instead of generating C++ code these procedures may produce a C++ code that will use a parser. A motivation of using the parser is that the compilation time of the program necessary to interval evaluate a complex expression may be very large (note that the procedure Auto_Diff, section 2.3.2, may allow to reduce this compilation time).
Each expression to evaluate will be written in a file and the interval evaluation will be done at run-time by parsing the file. This allow to deal with large expressions at a small cost. This is obtained by setting the variable `ALIAS/use_parser` along the following rules:
- 5: only the Hessian will be calculated using the parser
- 6: only the Jacobian and Hessian will be calculated using the parser
- 7: the expressions, their Jacobian and Hessian will be calculated using the parser
- 10: the expressions, their Jacobian and Hessian will be calculated using the parser
Improving the efficiency of the code
It may happen that the evaluation of an expression involves many time the
evaluation of a sub-expression. Clearly evaluating only once these
sub-expressions will speed up the code.
This may be done through a user-provided Maple procedure that must
be called ALIAS_FSIMPLIFY. This procedure takes as input a
file descriptor
and an expression expr. It will be first called right after the creation
of the evaluation file with a string: detecting that expr is a string
allow to write some initialization. Then it will be called before writing
any equation to allow for simplification.
For example assume that an expression that will be treated by the
Make[FJH] procedure involves numerous time the evaluation of the
sine and cosine of the first variable x (whose name in ALIAS-C++ is
v_IS(1)).The ALIAS_FSIMPLIFY procedure may be written as:
ALIAS_FSIMPLIFY:=proc(fid,expr)
local aux:
if type(expr,string) then
fprintf(fid,"INTERVAL SS,CC;\n"):
fprintf(fid,"SS=Sin(v_IS(1));\n"):
fprintf(fid,"CC=Cos(v_IS(1));\n"):
RETURN(0):
fi:
aux:=expr:
aux:=subs(sin(x)=SS,cos(x)=CC,aux):
RETURN(aux):
end:
This procedure will be first called with a string for expr and a
consequence is that at the beginning of the evaluation file fid
the interval variable SS,CC will be defined and then assigned to
the value of
The procedure Math_Func, see section 9.4, may be used to identify mathematical functions occurring in an expression and the list provided by this function may be used to write a generic ALIAS_FSIMPLIFY procedure that will automatically compute only once the more complex components of an expression. The procedure Auto_Diff, see section 2.3.2, may also be used to speed up the interval evaluation of an expression. Note also that a similar mechanism exists for expression involving determinants of matrices.
Function involving determinants
A determinant of a matrix A may appear in an equation using one of the syntax:
Fast_Determinant(A) Medium_Determinant(A) Slow_Determinant(A)the differences between the syntax being only in the computation time (from the fastest to the slowest) and in the width of the interval evaluation (from the largest to the narrowest). If you are interested in determining if a determinant may cancel you may also use Slow_NonZero_Determinant which is faster than Slow_Determinant.
Note that if determinants are present in the equations there are different ways to compute the determinant:
- by using Gaussian elimination. This method will be used only if the flag `ALIAS/use_gaussian_elim_det` is set to 1
- either by computing only the intervals for each component of the matrix and using a row or column expansion to determine the interval evaluation of the determinant
- same as above but the gradient of the coefficients are used to improve their interval evaluation
- by computing symbolically every minors of dimension
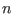 of the
matrix and using the interval evaluation of these expressions to
compute the interval evaluation of the determinant. The value of
of the
matrix and using the interval evaluation of these expressions to
compute the interval evaluation of the determinant. The value of 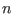 is given by `ALIAS/minor22 (default value: 2)
is given by `ALIAS/minor22 (default value: 2)
- a mix of method 2 and 3
Note that you may speed up the interval evaluation of functions including
determinant of matrices (which are often computer intensive) by
defining intermediate interval variables and substituting these
variables in the expression. For example assume that the coefficients
of a matrix A involve a large number of sine and cosine depending upon
the unknown ![]() , the first unknown in our list of unknowns:
you first define a Maple procedure intro_A
that return an
array of strings that contain all the definition of the intermediate
variables. In our case the procedure is:
, the first unknown in our list of unknowns:
you first define a Maple procedure intro_A
that return an
array of strings that contain all the definition of the intermediate
variables. In our case the procedure is:
intro_A=proc() local h; h:=["INTERVAL SX;SX=Sin(v_IS(1));","INTERVAL SY;SY=Cos(v_IS(1));"] RETURN(h); end:Note that the name of the unknowns in the code generated by ALIAS is v_IS. The two strings of the array h will be automatically inserted in the C++ procedure generated by ALIAS. Hence the intermediate variable SX, SY will contain the value of the interval evaluation of
simplify_A:=proc(eq) local eq1; eq1:=subs(Sin(v_IS(1))=SX,Cos(v_IS(1)=CX,eq): RETURN(eq1); end:
Dealing with undefined expressions
Not all expression may be evaluated using interval arithmetic. For
example expression involving a denominator whose interval evaluation
contain 0 cannot be evaluated. Similarly expressions involving square root of
terms whose lower bound is negative are not allowed. This does not
mean that such expressions cannot be dealt with ALIAS but that
the code must take care of such cases. The procedures MakeF and
MakeJ allows the user to deal with such cases. Note also that a
package described in section 2.1.5 allows one to to
produce automatically the procedures that are described in this section.
The purpose of the control mechanism is to allow the user to calculate the interval evaluation of terms that may cause a problem for the evaluation and if this a case to attribute a default value to the expression that use these terms. This is done directly at the level of the C++ code.
First of all it will be necessary to define some C++ interval that will be used during the auxiliary computation. MakeF will look at the string `ALIAS/user_FINIT` and if it is not of 0 length will write it directly after the beginning of the procedure. Hence writing:
`ALIAS/user_FINIT`:="INTERVAL U;":will allow to use the C++ interval U for the auxiliary computation. The procedure MakeJ uses for a similar purpose the variable `ALIAS/user_JINIT`. For the MakeF procedure the user will have to define a Maple procedure ALIAS_F that will be called before the generation of the C++ code of each equations or inequalities involved in the calculation. The syntax of this procedure is:
ALIAS_F:=proc(fid,i)where fid is the Maple file descriptor in which the C++ code is written and i is the number of the expression that is considered. This procedure allows to include some C++ code right before the evaluation of the expression i.
For example assume that you have a set of inequalities function of the variable x, y that are defined in the list INEQ and that some of these inequalities may have interval denominator. Hence before the evaluation it is necessary to check if the denominator evaluation may include 0, in which case the whole expression has to be evaluated to a large interval including 0 (indeed the algorithm of ALIAS will then consider that this inequality is not satisfied). An ALIAS_F procedure for this case may be written as:
ALIAS_F:=proc(fid,i)
global INEQ:
local j,aux:
# denom of inequality i is numeric: do nothing
if type(denom(op(1,INEQ[i])),numeric) then RETURN(0): fi:
# denom is not numeric, evaluate the denominator
aux:=denom(op(1,INEQ[i])):
#
#in the C++ evaluation procedure the unknown are in the table v_IS
aux:=subs(x=v_IS(1),y=v_IS(2),aux):
#substitute the mathematical operator by their interval equivalent
#using ALIAS procedure
aux:=`ALIAS/ReplaceText`("..",",",convert(aux,string)):
#write the denominator evaluation in the C++ file
fprintf(fid,"U=(%s);\n",aux):
#if the denominator evaluation include 0 return a large interval
#for expression i
fprintf(fid,"if((0<=U))V(%d)=INTERVAL(-1.e6,1.e6);\n",i):
#otherwise proceed with the real evaluation
fprintf(fid,"else\n"):
RETURN(0):
end:
Note that for MakeF the C++ evaluation of the i-th expression is
preceded by the label nexti (hence expression has label next2, expression 3 next3 and so on). Hence you may use a goto next3 to skip the evaluation of the second expression.
A similar mechanism is available for the MakeJ procedure. Before writing the code for the evaluation of the derivative of the expression i with respect to the unknown j the procedure ALIAS_J will be called. The syntax of this procedure is
ALIAS_J:=proc(fid,i,j)Note that in this case is compulsory to return a large interval if the evaluation cannot be done as the derivative may be used to improve the evaluation using a first order Taylor expansion. Note that the C++ procedure created by MakeJ evaluates the components of the jacobian element by element although it returns an interval matrix V.
Interval valuation and the Problem_Expression package
This package allows to deal automatically with expressions that cannot be evaluated using interval arithmetic for some range for the unknowns. Their purpose is to create ALIAS_F and ALIAS_J procedures that will be used by MakeF and MakeJ.
The first procedure in this package is Problem_Expression that will create a list A_CONSTS of constraints that must be verified to be able to evaluate an expression. The end-user may provide information on constraints that will always be satisfied by writing them in the global list variable A_CONSTS_ALWAYS_OK.
The syntax of Problem_Expression is:
Problem_Expression(expr)For example
Problem_Expression(x/(y-2)+sqrt(x+1));will produce the list
[y - 2 <> 0, -x - 1 <= 0]that indicates that the denominator of x/(y-2) must not include 0 and that the argument of sqrt cannot be an interval that includes negative numbers. Note that some element of this list of constraints may be used to speed up the solving of a problem by using the HullIConsistency procedure (see section 4.2.1) that will modify the ranges of the unknowns so that the expressions may be evaluated or even reject ranges for which one (or more) expression cannot be evaluated.
This procedure deals with the following evaluation problems:
- denominator that may include 0
- argument of square should be positive
- argument of arcsin and arccos should be included in [-1,1]
- argument of log,ln,log10 should be positive
- argument of arccosh should be greater than 1
- argument of arctanh cannot have an intersection with the interval [-1,1]
- argument
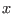 of
of 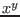 where
where 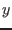 is not an integer should be positive
is not an integer should be positive
- argument
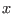 of
of 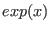 should not be too large to avoid
overflow problem.
should not be too large to avoid
overflow problem.
- if the constraint is
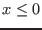 where
where
![$x=[\underline{x},\overline{x}]$](img13.png)
- if
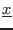 is positive expr will be
set to
[`ALIAS/low_value_expr_violated`,`ALIAS/high_value_expr_violated`]
is positive expr will be
set to
[`ALIAS/low_value_expr_violated`,`ALIAS/high_value_expr_violated`]
- if
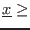 -`ALIAS/close_to_zero`
and
-`ALIAS/close_to_zero`
and
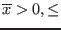 `ALIAS/close_to_zero` expr will be
set to [
`ALIAS/close_to_zero` expr will be
set to [
`ALIAS/low_value_expr_violated`, `ALIAS/high_value_expr_violated`] - if
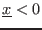 and
and 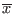 is positive expr will be set to the interval
[`ALIAS/lower_bound_uneval_expr`,
`ALIAS/upper_bound_uneval_expr`]
is positive expr will be set to the interval
[`ALIAS/lower_bound_uneval_expr`,
`ALIAS/upper_bound_uneval_expr`]
- if
- if the constraint is
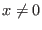
- if
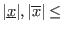 `ALIAS/close_to_zero` expr will be
set to [
`ALIAS/close_to_zero` expr will be
set to [
`ALIAS/low_value_expr_violated`, `ALIAS/high_value_expr_violated`] - if
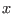 includes 0 or (
includes 0 or (
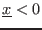 and
and
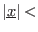 `ALIAS/close_to_zero`) or (
`ALIAS/close_to_zero`) or (
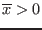 and
and
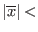 `ALIAS/close_to_zero`) expr will be set to the interval
[`ALIAS/lower_bound_uneval_expr`,
`ALIAS/upper_bound_uneval_expr`]
`ALIAS/close_to_zero`) expr will be set to the interval
[`ALIAS/lower_bound_uneval_expr`,
`ALIAS/upper_bound_uneval_expr`]
- if
- if the constraint is
![$x \cap [-1,1]=\emptyset$](img24.png) (for the arccoth
function) and
(for the arccoth
function) and 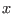 has an intersection with this interval then
expr will be set to the interval
[`ALIAS/lower_bound_uneval_expr`,
`ALIAS/upper_bound_uneval_expr`]
has an intersection with this interval then
expr will be set to the interval
[`ALIAS/lower_bound_uneval_expr`,
`ALIAS/upper_bound_uneval_expr`]
- if we deal with
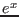
- if
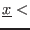 200 and
200 and
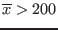 then expr is set to the
interval [
then expr is set to the
interval [
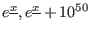 ]
]
- if
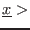 200 then xpr is set to
[
200 then xpr is set to
[
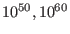 ]
]
- if
- if the constraint is
![$x \subset [-1,1]$](img31.png) (for the arcsin, arccos
functions) then
(for the arcsin, arccos
functions) then
- if
 or
or
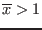 then expr will be
set to [
then expr will be
set to [
`ALIAS/low_value_expr_violated`, `ALIAS/high_value_expr_violated`] - if
 and
and
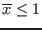 then
then 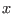 will be set to
will be set to
![$[-1,\overline{x}]$](img35.png)
- if
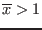 and
and
 then
then 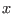 will be set to
will be set to
![$[\underline{x},1]$](img37.png)
- if
Verify_Problem_Expression(EQ,VAR)where EQ is a list of expressions and VAR a list of unknown names. The global list variable `ALIAS/Problems will contain the number of evaluation problems detected for each element of EQ.
This procedure generates also a C++ file ALIAS_F_AUTOMATIC.c with two procedures
- Is_Evaluable(INTERVAL_VECTOR X) that returns 1 if all the expressions in EQ can be evaluated when the unknown VAR have as range X
- Is_Evaluable(INTERVAL_VECTOR X), int i that returns 1 if all the i-th expression in EQ can be evaluated when the unknown VAR have as range X
If these procedures have been created, then the flag `ALIAS/has_test_evaluate` will be set to 1 (the procedure uses also the internal flag `ALIAS/test_evaluate`) to determine what should be done when a non-evaluability condition is satisfied for a given variable U. The code will be
if (non evaluable condition) {
U=default value;
goto next[i];} #if `ALIAS/test_evaluate`=0, i being computed
return 0;} #if `ALIAS/test_evaluate`=1
} #`ALIAS/test_evaluate`=2
goto next[i];} #`ALIAS/test_evaluate`=3, i =ALIAS_Next
U=real U value;
next[i]: ;
if (non evaluable condition) {
....
If `ALIAS/test_evaluate` is set to 3 the label number is given
by the global ALIAS variable ALIAS_Next.
These procedures may be used to test if an expression may be evaluated before using them for a filtering algorithm. For example the HullConsistency, HullIConsistency and Simp2B that implement the 2B filtering use automatically these procedures as soon as Verify_Problem_Expression has been called before their use (but Verify_Problem_Expression has to be called with the same list of unknowns and variables than the consistency procedures).
Note that Verify_Problem_Expression may have a third argument which is a string (e.g. "ALIAS_Coeff"). In that case instead of creating the ALIAS_F_AUTOMATIC file with the ALIAS_F Maple procedure the file ALIAS_Coeff will be created describing the Maple procedure ALIAS_Coeff(fid,i). If this procedure is called for expression i of func the procedure will create in the file described by fid the C++ code necessary to determine if this expression can be interval-valuated. If not then it is necessary to affect the i-th element of the interval vector that will be returned by the procedure. As we do not know the name of this vector it shall be indicated as the fourth argument of Verify_Problem_Expression. Hence
Verify_Problem_Expression(func ,Vars,"ALIAS_F_AUTOMATIC","V")is equivalent to Verify_Problem_Expression(func ,Vars). See an application of this use in section 8.3.
The Verify_Problem_ExpressionJ procedure creates in the same way a Maple procedure ALIAS_J. The rules are identical but the syntax of the procedure is
Verify_Problem_ExpressionJ(J,VAR)where J is an array that define the jacobian of EQ with respect to VAR. A typical call to this procedure is
with(linalg): J:=jacobian(EQ,VAR): Verify_Problem_ExpressionJ(eval(J),VAR)The name of the variables that allows one to specify what should be the return value of the expression are: `ALIAS/low_value_exprJ_violated`, `ALIAS/high_value_exprJ_violated`.
Note that in the C++ procedures generated by MakeF, MakeJ if an evaluation problem occurs the C++ flags ALIAS_ChangeF, ALIAS_ChangeJ will be set to 1 (default value 0) to indicate that the resulting computed value should be used with some care.
Interval evaluation of an expression in Maple
Maple provides the package evalr that calculate the interval evaluation of an expression. An example follows:
readlib(evalr): X:=INTERVAL(0..1): evalr(sin(X)*cos(X)+X);But this package does not evaluate correctly some expressions (for example X-X will be evaluated to 0 whatever is the interval for X). ALIAS-Maple provides the procedure Interval that allows for the interval evaluation of an expression as shown in the following example:
Interval([x*cos(y)+sin(x*y),x^2-cosh(y)],[x,y],[[-2,2],[-2,2]]);
[[[-3, 3]], [[-7.3890560989307,3.8646647167634]]]
The first argument is a list of expression, the second argument is the
name of the variables and the third a list of intervals for the variables.
The procedure generates a C++ program and hence may take some seconds.
But as soon as the executable has been created it is possible to
re-use it with other intervals using the Restart procedure
Restart("Interval",[[-0.5,0.5],[-0.5,0.5]]);
Note however that as soon as you have defined the `ALIAS/ID`
string
before generating an executable it is necessary to reset this string
to the same name before using the
Restart procedure to re-run the same executable
An optional 4th argument allows to control the evaluation. Indeed by default the expression will be transformed into a compact form (as provided by the procedure MinimalCout) that may lead to a better evaluation. The fourth argument may be:
- "AsIt": the expressions are not transformed and are evaluated as they are provided
- "Gradient": the derivatives of the expressions are used to try to improve the evaluation
Interval([x*sin(x)+cos(x)],[x],[[0,1]]);
[[[.54030230586814, 1.8414709848079]]]
Interval([x*sin(x)+cos(x)],[x],[[0,1]],"Gradient");
[[[1, 1.381773290676]]]
in which the use of the "Gradient" option allows to get the exact
interval evaluation.
It must be reminded that the interval evaluation of an expression is
very sensitive to the manner with which the expression is written. For
example the expression
Interval([x^2+2*x+1],[x],[[-1,1]],"AsIt");
[[[-1, 4]]]
If the option AsIt is not used ALIAS will convert the expression
into the Horner form
Interval([x^2+2*x+1],[x],[[-1,1]]);
[[[-2, 4]]]
Here it may be noticed that the Horner form leads to a worst interval
evaluation. But we may factor this expression as
Interval([(x+1)^2],[x],[[-1,1]],"AsIt");
[[[0, 4]]]
Generating code
Transforming expressions into C++ code
The BIAS/Profil C++ version of an arbitrary Maple expression may be obtained by using the procedure Code that will display on the standard output the C++ equivalent of the Maple expression. The syntax of this command is:
Code(eq); Code([eq1,eq2,eq3]);In the later case the components of the interval vector v_IS will be affected to each component in the list.
If this procedure has a second argument which is a list of variable the procedure will provide a C++ evaluation formula where the unknown has been substituted by the element of the interval vector v_IS (which the name of the interval vector used internally by ALIAS):
Code(x^2+2*x+1,[x]);
Sqr(v_IS(1)) + 2 v_IS(1) + 1
An optional last argument, the string "minimal" may be added: in that case the procedure will try to produce a compact form for the expression that may be more appropriate for interval evaluation and is the result of the procedure MinimalCout:
Code(x^2+2*x+1); v_IS=Sqr(x)+2*x+1; Code(x^2+2*x+1,"minimal"); v_IS=1+(2+x)*x;
Interval evaluation and Taylor remainder
The procedure Auto_Diff addresses two main problems:
- when dealing with large or complex expression the compilation time of the C++ program that is needed to interval evaluate the expression may be quite large
- for some problem it may be interesting to have a procedure that computes the Taylor remainder of a given expression. But this remainder may have a very large expression and the first item apply
Auto_Diff(Func,Vars,N,REM)where N is the order of the Taylor remainder (if N is set to 0 this remainder is the expression itself) and REM is a string that will be the name of the C++ program that will compute the remainder (the program is written in the file REM.c). Note that REM is a procedure using MakeF format.
As the remainder may be a very large expression but which includes multiple occurrences of the same elementary components Auto_Diff uses the Decompose_Diff procedure to reduce the number of interval evaluation of the same elementary components.
Consider the expression
and apply Auto_Diff for the evaluation of this expression
Auto_Diff((sin(x)^2+cos(x)^3)/x+x*(sin(x)^2+cos(x)^3),[x],0,"REM");
(ALIAS_B4 + ALIAS_B5) ALIAS_B1 + x (ALIAS_B4 + ALIAS_B5)
This indicates that the terms
The calculation of these dummy variables is done in the procedure ALIAS_DIFF.C:
#include <fstream.h>
#include "Functions.h"
#include "Vector.h"
#include "IntervalVector.h"
#include "IntervalMatrix.h"
#include "IntervalMatrix.h"
#include "IntegerVector.h"
#include "IntegerMatrix.h"
INTERVAL_VECTOR ALIAS_DIFF(INTERVAL_VECTOR &v_IS)
{
INTERVAL_VECTOR B(3);
INTERVAL_VECTOR AD(5);
Clear(AD);
B(1)=Sqr(Sin(v_IS(1)));
B(2)=Power(Cos(v_IS(1)),3);
B(3)=1/v_IS(1);
AD(1)=B(3);
AD(2)=B(1);
AD(3)=B(2);
AD(4)=B(1);
AD(5)=B(2);
return AD;
}
Note that ALIAS_DIFF.C is a self-contained program that can be
compiled independently. The code for REM.c is
INTERVAL_VECTOR ALIAS_DIFF(INTERVAL_VECTOR &v_IS);
#include "ALIAS_REM.c"
INTERVAL_VECTOR REM(int l1,int l2,INTERVAL_VECTOR & v_IS)
{
INTERVAL_VECTOR V(1),X(5),XX(6);
int i;
//computation of the elementary components
X=ALIAS_DIFF(v_IS);
for(i=1;i<=1;i++)XX(i)=v_IS(i);
for(i=1;i<=5;i++)XX(i+1)=X(i);
//XX contains the unknowns and then the elementary components
V=ALIAS_REM(1,1,XX);
return V;
}
Here the interval vector XX contains first the variable and then
the dummy variables. The calculation of the expression is then
performed by the ALIAS_REM procedure:
INTERVAL_VECTOR ALIAS_REM(int l1, int l2, INTERVAL_VECTOR & v_IS) {
INTERVAL_VECTOR V(1);
next1:
if (l1<=1 && 1<=l2)
{
V(1)=(v_IS(5)+v_IS(6))*v_IS(2)+v_IS(1)*(v_IS(5)+v_IS(6));
}
next2: ;
return V;
}
For a remainder let's use
Auto_Diff((sin(x)^2+cos(x)^3)/x+x*(sin(x)^2+cos(x)^3),[x],1,"REM");which returns
(ALIAS_B4 ALIAS_B3 + ALIAS_B7 + ALIAS_B8 + ALIAS_B4 ALIAS_B2
+ (ALIAS_B7 + ALIAS_B8) ALIAS_B1 + x (ALIAS_B3 + ALIAS_B2)) W_x_1
Here W_x_1 represents Note that Auto_Diff try to improve the interval evaluation by using a Horner form. But it can be seen that it does not always provide the best one. In the previous example
((ALIAS_B7 + ALIAS_B8)(1+ ALIAS_B1) + (x+ALIAS_B4) (ALIAS_B3 + ALIAS_B2)) W_x_1will have been optimal.