Customizing and improving the code produced by ALIAS-Maple
Source code
The source code produced by ALIAS-Maple may be customized to improve the efficiency. The name of the programs that are produced by the ALIAS Maple library follows some simple rules:
- _G*.C: name of the main program for the non-parallel implementation. The characters following G vary according to the procedure
- _F*.c: name of the program providing the equation evaluation
- _J*.c: name of the program providing the estimation of the gradient of the equation
- _H*.c: name of the program providing the estimation of the Hessian of the equation
- _makefile*: name of the make program
- _Sol_, _Func_: result of the computation
- _MASTER*.C: master main program for parallel implementation
- _SLAVE*.C: slave main program for the parallel implementation
- _sys_,_temp_,_Func_ : auxiliary files, may be removed at will
Some rules to improve efficiency
Function evaluation
- when formulating your problem find the best compromise between the number of equations and their complexity. Having the lowest possible number of equations may not be the best if the equations are very complex
- remember that you are not stuck to algebraic equations
- first focus on the problem at hand, not on the equations (see the example in the next section and the example in section 13.2.3.1)
- give the equations from the simplest to the more complex
- if you are using methods involving the gradient and have equations that are similar in the number of terms give first the equations that may have a gradient with a constant sign
- try to factor our most of the term (e.g.
 will in
general be better than
will in
general be better than  ). ALIAS-Maple will try to do this
job for you but any help is welcome!
). ALIAS-Maple will try to do this
job for you but any help is welcome!
- try to normalize your equation and variable
A counter-example
ALIAS-Maple is designed to help generating C++ code and improving the efficiency of the algorithm. But it will not solve all the problems that may be treated by interval analysis as illustrated by the following example that originated from the Geometrica project.
Consider 2 ellipses E1, E2 in the plane that are perfectly defined and the
so-called bi-tangent i.e. the lines that are tangent to both
ellipsis. There is 4 such lines but we assume that some criteria
allows to choose two bi-tangents L1, L2. L1 intersects E1 at point P,
E2 at and L2 intersects E1 at point R and E2 at point S. We construct
now the vectors PQ, RS and then the determinant
D=![]() PQ RS
PQ RS![]() . The problem is to determine the sign of D in a
guaranteed manner (this sign is then used for another algorithm and a
mistake in the sign has a very negative influence).
. The problem is to determine the sign of D in a
guaranteed manner (this sign is then used for another algorithm and a
mistake in the sign has a very negative influence).
A classical approach to solve this problem is to consider that the 8 coordinates of the points P, Q, R, S are the unknowns, write 8 equations to determine these unknowns, solve the system and then determine the sign of D. But this approach has drawbacks:
- the system of equations is complex
- it is difficult to solve exactly
Now we may note that the coordinates of the points are bounded as the points are included in the bounding box of the ellipses. Being given ranges for the unknowns we may compute the interval evaluation of the determinant. If the lower bound is positive or the upper bound is negative we may directly state the sign of the determinant. If not we bisect one the unknown coordinates: we has thus a list of boxes with 8 ranges in each box, one for each coordinate. For each box we check if the coordinates ranges allows the points P, Q, R, S to belong to the ellipsis and to the bi-tangents, otherwise we reject the box. Then we compute the interval evaluation of D: if the lower bound is positive we store the box in a special array of boxes, called the positive array and discard it from the list. Similarly if the upper bound is negative we store the box in the negative array and discard it from the list. When the list of boxes is exhausted we look at the number of elements in the positive and negative array: if one array has 0 element, then we have determined the sign of D. Otherwise we consider the array that has the lowest number of elements and restart the bisection procedure on this new list, eliminating boxes that do not describe points on the ellipsis or that are not on the bi-tangent. At the end of this process we may have eliminated all the boxes of the list or, in the worst case, we will have computed the coordinates of P, Q, R, S i.e. we will end up with the classical approach. Our test show however that this is seldom the case and the above procedure is much more faster than solving using the classical approach.
Still in some cases the sign of D cannot be safely computed: this may happen for example when some coordinates have very large values while other have very small one. Numerical round-off errors then prohibit the exact determination of the sign of D, a fact that is detected by interval analysis. But we may still in some cases solve the problem: for that purpose instead of using Cartesian coordinates we may use polar coordinates with different ranges for the unknowns in the determinant or we may use an extended arithmetic. In any case the algorithm is safe as it provides either a sign, which is guaranteed, or will state that the sign cannot be determined with the current arithmetic.
In this example the MakeF, MakeJ procedures may be used to generate the C++ code for evaluating the value of D and to check if the points belong to the ellipsis. But then specific C++ code should be written, mostly based on the ALIAS-C++ library.
Simplification procedures
- introduce any a-priori simplification rules
- use the 3B and 2B consistency approach. You may start using the
HullConsistency and Simp2B procedure but
you may still have a lot of
opportunity to produce efficient simplification procedure. For example
if you have an
expression like
 you may write down
(provided that
you may write down
(provided that
 is a range that does not contain 0)
is a range that does not contain 0)
 and consider as new range for
and consider as new range for 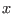 the intersection of U with the
current range for
the intersection of U with the
current range for