Public Member Functions
template<class Poly >
C	lower_bound (const Poly &f) const
	Computes the Cauchy lower bound on the first positive root as a power of 2. More...

template<class Poly >
long	lower_power_2 (const Poly &f) const

template<>
double	upper_bound (const Poly &p)

Static Public Member Functions
template<class Poly >
static C	upper_bound (const Poly &p)
	Computes the Cauchy root bound. More...

Detailed Description

Cauchy bound.

Member Function Documentation

template<class C>

template<class Poly >

C mmx::Cauchy< C >::lower_bound ( const Poly & f ) const

inline

Computes the Cauchy lower bound on the first positive root as a power of 2.

Parameters

f	Univariate polynomial

template<class C>

template<class Poly >

long mmx::Cauchy< C >::lower_power_2 ( const Poly & f ) const

inline

template<class C>

template<class Poly >

static C mmx::Cauchy< C >::upper_bound ( const Poly & p )

inlinestatic

Computes the Cauchy root bound.

Parameters

p	Univariate polynomial

Poly is the type of the polynomial. C is the type of the result.

If the polynomial p is in the monomial basis is of the form

$p(x) = a_{0} + a_{1} x+ \cdots + a_{d}\, x^d,$

the Cauchy bound on the modul of the roots of 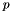$p$ is

$1 + max{|a_{0}|,...,|a_{d-1}|}/|a_{d}|$

template<>

double mmx::Cauchy< double >::upper_bound ( const Poly & p )

The documentation for this struct was generated from the following file: