shape_doc 0.1
Public Types | Public Member Functions | Public Attributes | Protected Attributes
cell2d_voronoi_diagram< C, V > Class Template Reference

#include <cell2d_voronoi_diagram.hpp>

Inheritance diagram for cell2d_voronoi_diagram< C, V >:
cell2d< C, V > cell< C, REF_OF(V) > bounding_box< C, REF_OF(V) > Shape

List of all members.

Public Types

Public Member Functions

Public Attributes

Protected Attributes

Detailed Description

template<class C, class V = default_env>
class mmx::shape::cell2d_voronoi_diagram< C, V >

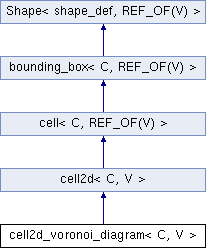
Definition at line 41 of file cell2d_voronoi_diagram.hpp.

Member Typedef Documentation

typedef cell<C,V>::BoundingBox BoundingBox

Reimplemented from cell2d< C, V >.

Definition at line 47 of file cell2d_voronoi_diagram.hpp.

typedef cell<C, REF_OF(V) > Cell [inherited]

Reimplemented in cell2d_algebraic_curve< C, V >, cell2d_parametric_curve< C, V >, and cell2d_voronoi_site2d< C, V >.

Definition at line 65 of file cell2d.hpp.

typedef Interval<double> coeff

Definition at line 53 of file cell2d_voronoi_diagram.hpp.

typedef topology2d<C,V>::Edge Edge

Reimplemented from cell2d< C, V >.

Definition at line 49 of file cell2d_voronoi_diagram.hpp.

typedef cell2d<C,V>::Point Point

Reimplemented from cell2d< C, V >.

Definition at line 48 of file cell2d_voronoi_diagram.hpp.

typedef polynomial< Interval<double>, with<Bernstein> > Polynomial

Definition at line 52 of file cell2d_voronoi_diagram.hpp.

typedef topology<C,V> Topology

Reimplemented from cell2d< C, V >.

Definition at line 50 of file cell2d_voronoi_diagram.hpp.

typedef use<cell_def,REF_OF(V) > VARIANT [inherited]

Definition at line 57 of file cell.hpp.

Constructor & Destructor Documentation

cell2d_voronoi_diagram ( void  )

Definition at line 637 of file cell2d_voronoi_diagram.hpp.

: m_intersected(false), m_treated(false) {}
cell2d_voronoi_diagram ( double  xmin,
double  xmax 
)
cell2d_voronoi_diagram ( double  xmin,
double  xmax,
double  ymin,
double  ymax 
)

Definition at line 640 of file cell2d_voronoi_diagram.hpp.

:  cell2d<C,V>(xmin, xmax, ymin, ymax), m_intersected(false), m_bisector(false), m_treated(false) {}
cell2d_voronoi_diagram ( double  xmin,
double  xmax,
double  ymin,
double  ymax,
bool  itr 
)

Definition at line 643 of file cell2d_voronoi_diagram.hpp.

: cell2d<C,V>(xmin, xmax, ymin, ymax), m_intersected(itr), m_bisector(false), m_treated(false) {}
cell2d_voronoi_diagram ( const BoundingBox &  bx)

Definition at line 646 of file cell2d_voronoi_diagram.hpp.

: cell2d<C,V>(bx), m_intersected(false), m_bisector(false), m_treated(false)  {};
~cell2d_voronoi_diagram ( void  ) [virtual]

Definition at line 649 of file cell2d_voronoi_diagram.hpp.

                                  {
    foreach (Cell* m, this->m_objects) delete m;
}

Member Function Documentation

void addsite ( unsigned  i) [inline]

Definition at line 165 of file cell2d_voronoi_diagram.hpp.

{m_sites<<i;};
BoundingBox boundingBox ( ) const [inline, inherited]

Definition at line 88 of file cell.hpp.

{ return (BoundingBox)*this; }
virtual Point center ( void  ) const [inline, virtual, inherited]

Definition at line 82 of file cell.hpp.

                                         { 
    // XXX ???
    return Point(this->xmax()-this->xmin(),
                 this->ymax()-this->ymin(),
                 this->zmax()-this->zmin()); 
  }
bool compute_boundary ( ) [inline]

Definition at line 371 of file cell2d_voronoi_diagram.hpp.

References Cell2d, Cell2dAlgebraicCurve, cell2d< C, V >::e_neighbors, cell2d_voronoi_diagram< C, V >::intersections(), cell2d_voronoi_diagram< C, V >::m_bisector, cell2d_voronoi_diagram< C, V >::m_objects, cell2d_voronoi_diagram< C, V >::m_sites, cell2d_voronoi_diagram< C, V >::m_treated, cell2d< C, V >::n_neighbors, cell2d< C, V >::s_neighbors, SELF, cell2d< C, V >::w_neighbors, point< C, V, N >::x(), bounding_box< C, REF_OF(V) >::xmax(), bounding_box< C, REF_OF(V) >::xmin(), point< C, V, N >::y(), bounding_box< C, REF_OF(V) >::ymax(), and bounding_box< C, REF_OF(V) >::ymin().

{
  int i(0),j(0), r(m_sites.size()-1);
  foreach ( Cell* obj, this->m_objects)
  {
    Cell2dAlgebraicCurve* cc= dynamic_cast<Cell2dAlgebraicCurve*>(obj);
    if (j<r) // bisector signature (i,j)
      j++;
    else
      { i++; j=i+1;}

    //0
    if ( this->s_neighbors.size()==0)
    {
      Seq<Point *> ip;
        Solver::edge_point(ip,
                           cc->m_polynomial,
                           Solver::south_edge, 
                           *cc);
        cc->s_intersections << ip;
      }
    else
      foreach( Cell2d *c, this->s_neighbors )
        if  ( ((SELF*)c)->m_bisector ) 
        {
          Seq<unsigned> a= ((SELF*)c)->sites();
            if ( a.member( m_sites[i]) && a.member(m_sites[j]) )
            {
              foreach(Point * p, ((SELF*)c)->intersections(2) ) 
                if (this->xmin()<p->x() && this->xmax()>p->x())
                  cc->s_intersections << p;
            }
          }
        else if ( ((SELF*)c)->m_treated )
        {
              int u(0),v(0);
              foreach( Cell *nc, ((SELF*)c)->m_objects )
              {
                if (v<r) // bisector signature (u,v)
                  v++;
                else
                { u++; v=u+1;}
                  if ( ((SELF*)c)->m_sites[u]==m_sites[i] && 
                       ((SELF*)c)->m_sites[v]==m_sites[j] )
              foreach(Point * p, ((SELF*)nc)->intersections(2) ) 
                if (this->xmin()<p->x() && this->xmax()>p->x())
                  cc->s_intersections << p;
          }
       }
        else
        {
          Seq<Point *> ip;
            Solver::edge_point(ip,
                               cc->m_polynomial,
                               Solver::south_edge, 
                               *cc  );
            foreach(Point * p, ip ) 
              if (c->xmin()<p->x() && c->xmax()>p->x())
                cc->s_intersections << p;
            //std::cout<<"ip: "<< ip.size() <<"\n";
          }
        
        //1
        if (this->e_neighbors.size()==0)
        {
          Seq<Point *> ip;
            Solver::edge_point(ip,
                               cc->m_polynomial,
                               Solver::east_edge, 
                               *cc);
               cc->e_intersections << ip;
          }
        else
          foreach( Cell2d *c, this->e_neighbors )
            if ( ((SELF*)c)->m_bisector ) 
            {
              Seq<unsigned> a= ((SELF*)c)->sites();
              if ( a.member( m_sites[i]) && a.member(m_sites[j]) )
              {
                foreach(Point * p, ((SELF*)c)->intersections(3) ) 
                  if (this->ymin()<p->y() && this->ymax()>p->y())
                    cc->e_intersections << p;
              }
            }
            else if ( ((SELF*)c)->m_treated )
            {
              int u(0),v(0);
              foreach( Cell *nc, ((SELF*)c)->m_objects )
              {
                if (v<r) // bisector signature (u,v)
                  v++;
                else
                { u++; v=u+1;}
                  if ( ((SELF*)c)->m_sites[u]==m_sites[i] && 
                       ((SELF*)c)->m_sites[v]==m_sites[j] )
                    foreach(Point * p, ((SELF*)nc)->intersections(3) ) 
                      if (this->ymin()<p->y() && this->ymax()>p->y())
                        cc->e_intersections << p;                    
                    }
              }
            else
            {
              Seq<Point *> ip;
                Solver::edge_point(ip,
                                   cc->m_polynomial,
                                   Solver::east_edge, 
                                   *cc  );
                 foreach(Point * p, ip ) 
                   if (c->ymin()<p->y() && c->ymax()>p->y())
                     cc->e_intersections << p;
              }
            
            //2
             if (this->n_neighbors.size()==0 )
             {
               Seq<Point *> ip;
                 Solver::edge_point(ip,
                                    cc->m_polynomial,
                                    Solver::north_edge, 
                                    *cc);
                 cc->n_intersections << ip;
               }
             else
               foreach( Cell2d *c, this->n_neighbors )
                 if ( ((SELF*)c)->m_bisector ) 
                 {
                   Seq<unsigned> a= ((SELF*)c)->sites();
                     if ( a.member( m_sites[i]) && a.member(m_sites[j]) )
                     {
                   foreach(Point * p, ((SELF*)c)->intersections(0) ) 
                     if (this->xmin()<p->x() && this->xmax()>p->x())
                       cc->n_intersections << p;
                     }
                   }
            else if ( ((SELF*)c)->m_treated )
            {
              int u(0),v(0);
              foreach( Cell *nc, ((SELF*)c)->m_objects )
              {
                if (v<r) // bisector signature (u,v)
                  v++;
                else
                { u++; v=u+1;}
                  if ( ((SELF*)c)->m_sites[u]==m_sites[i] && 
                       ((SELF*)c)->m_sites[v]==m_sites[j] )
                   foreach(Point * p, ((SELF*)nc)->intersections(0) ) 
                      if (this->xmin()<p->x() && this->xmax()>p->x())
                        cc->n_intersections << p;                    
                }
              }
                 else
                 {
                   Seq<Point *> ip;
                     Solver::edge_point(ip,
                                        cc->m_polynomial,
                                        Solver::north_edge, 
                                        *cc );
                     foreach(Point * p, ip ) 
                       if (c->xmin()<p->x() && c->xmax()>p->x())
                         cc->n_intersections << p;
                   }
                 
                 //3
                 if (this->w_neighbors.size()==0)
                 {
                   Seq<Point *> ip;
                 Solver::edge_point(ip,
                                    cc->m_polynomial,
                                    Solver::west_edge, 
                                    *cc);
                 cc->w_intersections << ip;
               }
                 else
               foreach( Cell2d *c, this->w_neighbors )
                 if ( ((SELF*)c)->m_bisector ) 
                 {
                   Seq<unsigned> a= ((SELF*)c)->sites();
                     if ( a.member( m_sites[i]) && a.member(m_sites[j]) )
                     {
                   //Cell2d *c;
                   //foreach(Point * p, ((VSite*)( ((SELF*)c)->m_objects[0]))->e_intersections ) 
                   foreach(Point * p, ((SELF*)c)->intersections(1) ) 
                     if (this->ymin()<p->y() && this->ymax()>p->y())
                       cc->w_intersections << p;
                     }
                   }
            else if ( ((SELF*)c)->m_treated )
            {
              int u(0),v(0);
              foreach( Cell *nc, ((SELF*)c)->m_objects )
              {
                if (v<r) // bisector signature (u,v)
                  v++;
                else
                { u++; v=u+1;}
                  if ( ((SELF*)c)->m_sites[u]==m_sites[i] && 
                       ((SELF*)c)->m_sites[v]==m_sites[j] )
                   foreach(Point * p, ((SELF*)nc)->intersections(1) ) 
                     if (this->ymin()<p->y() && this->ymax()>p->y())
                       cc->w_intersections << p;                    
                    }
              }
                 else
                 {
                   Seq<Point *> ip;
                     Solver::edge_point(ip,
                                        cc->m_polynomial,
                                        Solver::west_edge, 
                                        *cc  );
                     foreach(Point * p, ip ) 
                       if (c->ymin()<p->y() && c->ymax()>p->y())
                         cc->w_intersections << p;
                     
                     //std::cout<<"west: "<< *ip[0] <<"\n";
                   }
                 
        }
  this->m_treated=true;
  return true;
}//compute_boundary
void connect0 ( cell2d< C, V > *  a,
cell2d< C, V > *  b 
) [inline, inherited]

Definition at line 281 of file cell2d.hpp.

References mmx::shape::check_overlap(), and SELF.

{
    int i;
    bool flag;

    //copy horizontally
    b->e_neighbors= this->e_neighbors ;
    foreach(SELF* cl,b->e_neighbors) {
        i= cl->w_neighbors.search(this);
        cl->w_neighbors[i]= b;
    }
    a->w_neighbors= this->w_neighbors ;
    foreach(SELF* cl,a->w_neighbors) {
        i= cl->e_neighbors.search(this);
        cl->e_neighbors[i]= a;
    }

    //update vertically
    foreach(SELF* cl,this->s_neighbors) {
        flag=false;
        if ( check_overlap(cl,a,0))
        {
          //assert( cl->ymax()== a->ymin() );
            a->s_neighbors<< cl;
            i= cl->n_neighbors.search(this);
            cl->n_neighbors[i]= a;
            flag=true;
        }
        if ( check_overlap(cl,b,0) )
        {
          //assert( cl->ymax()== b->ymin() );
            b->s_neighbors<< cl;
            if (!flag)
            {
                i= cl->n_neighbors.search(this);
                cl->n_neighbors[i]= b;
            }
            else
                cl->n_neighbors << b;
        }
    }
    foreach(SELF* cl,this->n_neighbors) {
        flag=false;
        if ( check_overlap(cl,a,0)) 
        {
            a->n_neighbors<< cl;
            i= cl->s_neighbors.search(this);
            cl->s_neighbors[i]= a;
            flag=true;
        }
        if ( check_overlap(cl,b,0) )
        {
            b->n_neighbors<< cl;
            if (!flag)
            {
                                        i= cl->s_neighbors.search(this);
                                        cl->s_neighbors[i]= b;
            }
            else
                                        cl->s_neighbors << b;
        }
  }
}
void connect1 ( cell2d< C, V > *  a,
cell2d< C, V > *  b 
) [inline, inherited]

Definition at line 346 of file cell2d.hpp.

References mmx::shape::check_overlap(), and SELF.

{
    int i;
    bool flag;

    //copy vertically
   a->s_neighbors= this->s_neighbors ;
     foreach(SELF* cl,a->s_neighbors) {
        i= cl->n_neighbors.search(this);
        cl->n_neighbors[i]= a;
    }
    b->n_neighbors= this->n_neighbors ;
    foreach(SELF* cl,b->n_neighbors) {
        i= cl->s_neighbors.search(this);
        cl->s_neighbors[i]= b;
    }

    //update horizontally
    foreach(SELF* cl,this->w_neighbors) {
            flag=false;
            if ( check_overlap(cl,a,1)) 
            {
                //assert( cl->xmax()== a->xmin() );
                a->w_neighbors<< cl;
                i= cl->e_neighbors.search(this);
                cl->e_neighbors[i]= a;
                flag=true;
            }
            if ( check_overlap(cl,b,1) )
            {
                //assert( cl->xmax()== b->xmin() );
                b->w_neighbors<< cl;
                if (!flag)
                {
                    i= cl->e_neighbors.search(this);
                    cl->e_neighbors[i]= b;
                }
                else
                    cl->e_neighbors << b;
            }
    }
    foreach(SELF* cl,this->e_neighbors) {
        flag=false;
        if ( check_overlap(cl,a,1)) 
        {
            a->e_neighbors<< cl;
            i= cl->w_neighbors.search(this);
            cl->w_neighbors[i]= a;
            flag=true;
        }
        if ( check_overlap(cl,b,1) )
        {
            b->e_neighbors<< cl;
            if (!flag)
            {
                i= cl->w_neighbors.search(this);
                cl->w_neighbors[i]= b;
            }
            else
                cl->w_neighbors << b;
        }
    }
}
bool contains ( double  x,
bool  strict = false 
) [inherited]
bool contains ( double  x,
double  y,
bool  strict = false 
) [inherited]
bool contains ( double  x,
double  y,
double  z,
bool  strict = false 
) [inherited]
int count ( void  ) [inline]

Definition at line 115 of file cell2d_voronoi_diagram.hpp.

References cell2d_voronoi_diagram< C, V >::m_objects.

Referenced by cell2d_voronoi_diagram< C, V >::signof(), and cell2d_voronoi_diagram< C, V >::site().

{ return m_objects.size() ; }
void disconnect ( ) [inline, inherited]

Definition at line 422 of file cell2d.hpp.

{
    this->e_neighbors.clear();
    this->w_neighbors.clear();
    this->n_neighbors.clear();
    this->s_neighbors.clear();
}
Polynomial func ( const int  i) const [inline]

Definition at line 116 of file cell2d_voronoi_diagram.hpp.

References cell2d_voronoi_diagram< C, V >::m_objects, and VSite.

                                              {
       return ((VSite*)(this->m_objects[0]))->m_polynomial;
     };
bool insert_regular ( Topology *  s) [virtual]

Implements cell< C, REF_OF(V) >.

Definition at line 684 of file cell2d_voronoi_diagram.hpp.

References Cell2d, Cell2dAlgebraicCurve, Edge, EPSILON, topology< C, V >::insert(), cell< C, V >::is_active(), mmx::shape::print(), SELF, and VSite.

                                {

  Seq<Point*> l;
  l= this->intersections();

  
  //std::cout<<"VD, regular: "<< *this<<", #="<<l.size() <<std::endl;
  // foreach( Point* e, l)
  //    std::cout<<*e <<", at "<< e <<std::endl;

  int * sz;
  int * st;
  Point *q;

  if ( l.size()==2 )
  {
    s->insert( l[0] );
    s->insert( l[1] );
    s->insert( new Edge(l[0],l[1]) );
    return true;
  }

  if ( l.size()==4 ) // two dublicated
  {
    s->insert( l[0] );
    s->insert( l[1] );
    s->insert( new Edge(l[0],l[1]) );
    return true;
  }
  
  if ( l.size()==1)
  {
    std::cout<< "SIZE ONE, "<< *this<<std::endl;

    s->insert( l[0] );
    foreach( Cell* c, this->m_objects )
      if ( ((Cell2d*)c)->nb_intersect()==1 )
      {
        sz= ((VSite*)c)->m_polynomial.rep().szs();
        st= ((VSite*)c)->m_polynomial.rep().str();
        if ( ((VSite*)c)->m_polynomial[0]<EPSILON )
        {
          q= new Point(this->xmin(),this->ymin(),0); 
          std::cout<< "1.add ("<< *q <<")->("<< *l[0] << ") in "<< *this<<std::endl;
          s->insert(q);
          s->insert( new Edge(l[0],q) );
          ((VSite*)c)->n_intersections<< q;

          foreach( Cell2d *nb, this->s_neighbors )
            foreach( Cell* cc, ((SELF*)nb)->m_objects )
            if ( cc->is_active() )
            {
              ((VSite*)cc)->n_intersections<< q;
              std::cout<<"This Intersections: "<< this->intersections().size() << std::endl;
              std::cout<<"Neib Intersections: "<< nb->intersections().size() << std::endl;
              return true;
            }
          foreach( Cell2d *nb, this->w_neighbors )
            foreach( Cell* cc, ((SELF*)nb)->m_objects )
            if ( cc->is_active() )
            {
              ((VSite*)cc)->e_intersections<< q;
              std::cout<<"This Intersections: "<< this->intersections().size() << std::endl;
              std::cout<<"Neib Intersections: "<< nb->intersections().size() << std::endl;
              return true;
            }

        } else if ( ((VSite*)c)->m_polynomial[(sz[0]-1)*st[0]]<EPSILON )
        {
          q= new Point(this->xmax(),this->ymax(),0);
          std::cout<< "2.add ("<< *q <<")->("<< *l[0] << ") in "<< *this<<std::endl;
          s->insert(q);
          s->insert( new Edge(l[0],q) );
          ((VSite*)c)->s_intersections<< q;


          foreach( Cell2d *nb, this->e_neighbors )
            foreach( Cell* cc, ((SELF*)nb)->m_objects )
            if ( cc->is_active() )
            {
              ((VSite*)cc)->w_intersections<< q;
              std::cout<<"This Intersections: "<< this->intersections().size() << std::endl;
              std::cout<<"Neib Intersections: "<< nb->intersections().size() << std::endl;
              return true;
            }
          foreach( Cell2d *nb, this->n_neighbors )
            foreach( Cell* cc, ((SELF*)nb)->m_objects )
            if ( cc->is_active() )
            {
              ((VSite*)cc)->s_intersections<< q;
              std::cout<<"This Intersections: "<< this->intersections().size() << std::endl;
              std::cout<<"Neib Intersections: "<< nb->intersections().size() << std::endl;
              return true;
            }

        } else if ( ((VSite*)c)->m_polynomial[sz[0]*sz[1]-1]<EPSILON )
        {
          q= new Point(this->xmin(),this->ymax(),0);
          std::cout<< "3.add ("<< *q <<")->("<< *l[0] << ") in "<< *this<<std::endl;
          s->insert(q);
          s->insert( new Edge(l[0],q) );
          ((VSite*)c)->w_intersections<< q;
          return true;
        } else if ( ((VSite*)c)->m_polynomial[(sz[1]-1)*st[1]]<EPSILON )
        {
          q= new Point(this->xmax(),this->ymin(),0);
          std::cout<< "4.add ("<< *q <<")->("<< *l[0] << ") in "<< *this<<std::endl;
          s->insert(q);
          s->insert( new Edge(l[0],q) );
          ((VSite*)c)->e_intersections<< q;
          return true;
        }  
      }
  }

  if ( l.size()==0)
  {
    std::cout<< "SIZE ZERO, "<< *this<<std::endl;
    return true;

    foreach( Cell* c, this->m_objects )
      {
        sz= ((VSite*)c)->m_polynomial.rep().szs();
        st= ((VSite*)c)->m_polynomial.rep().str();
        if ( ((VSite*)c)->m_polynomial[0]<EPSILON )
        {
          q= new Point(this->xmin(),this->ymin(),0); 
          std::cout<< "1.add ("<< *q <<") in "<< *this<<std::endl;
          s->insert(q);
          ((VSite*)c)->n_intersections<< q;
          return true;
        } else if ( ((VSite*)c)->m_polynomial[(sz[0]-1)*st[0]]<EPSILON )
        {
          q= new Point(this->xmax(),this->ymax(),0);
          std::cout<< "1.add ("<< *q <<") in "<< *this<<std::endl;
          s->insert(q);
          ((VSite*)c)->s_intersections<< q;
          return true;
        } else if ( ((VSite*)c)->m_polynomial[sz[0]*sz[1]-1]<EPSILON )
        {
          q= new Point(this->xmin(),this->ymax(),0);
          std::cout<< "1.add ("<< *q <<") in "<< *this<<std::endl;
          s->insert( new Edge(l[0],q) );
          ((VSite*)c)->w_intersections<< q;
          return true;
        } else if ( ((VSite*)c)->m_polynomial[(sz[1]-1)*st[1]]<EPSILON )
        {
          q= new Point(this->xmax(),this->ymin(),0);
          std::cout<< "1.add ("<< *q <<") in "<< *this<<std::endl;
          s->insert(q);
          s->insert( new Edge(l[0],q) );
          ((VSite*)c)->e_intersections<< q;
          return true;
        }  
      }
  }

    std::cout<< "nb_in= "<<  this->nb_intersect() <<std::endl;
    //std::cout<< "box  = "<< *this <<std::endl;
        //foreach(Point* q, this->intersections() ) 
        //std::cout<< " "<< *q <<std::endl;
    print((Cell2dAlgebraicCurve*)m_objects[0]);
    return true;
}
virtual bool insert_singular ( Topology *  ) [inline, virtual]

Implements cell< C, REF_OF(V) >.

Definition at line 69 of file cell2d_voronoi_diagram.hpp.

{return false;};// not used
bounding_box<C,REF_OF(V) >* intersect ( const bounding_box< C, REF_OF(V) > &  other) [inherited]
void intersected ( bounding_box< C, REF_OF(V) > *  other) [inherited]
virtual Seq<Point *> intersections ( int  i) const [inline, virtual]

Reimplemented from cell2d< C, V >.

Definition at line 86 of file cell2d_voronoi_diagram.hpp.

References Cell2dAlgebraicCurve, and cell2d_voronoi_diagram< C, V >::m_objects.

                                                 {
      Seq<Point*> l;
      Cell2dAlgebraicCurve* c;
      
      foreach(Cell*m, this->m_objects)
      {
          c = dynamic_cast<Cell2dAlgebraicCurve*>(m);
          l<< c->intersections(i);
      }
      return l;
  }
Seq< typename mmx::shape::cell2d< C, V >::Point * > intersections ( ) const [virtual]

Reimplemented from cell2d< C, V >.

Definition at line 1182 of file cell2d_voronoi_diagram.hpp.

References Cell2d.

Referenced by cell2d_voronoi_diagram< C, V >::compute_boundary().

                         {
    Seq<Point *> s,e,n,w,r;
    //std::cout<<"intersections, "<<*this<<std::endl;
    Cell2d* cl;
    foreach (Cell* m, m_objects)
    {
        cl = dynamic_cast<Cell2d*>(m);           
        s<< cl->s_intersections;
        e<< cl->e_intersections;
        n<< cl->n_intersections;
        w<< cl->w_intersections;
    }
    s.sort(this->coord<0>);
    e.sort(this->coord<1>);
    n.sort(this->coord<0>);
    w.sort(this->coord<1>);

    r<<s;
    r<<e;
    r<<n.reversed();
    r<<w.reversed();


    return ( r ); 
}
bool intersects ( bounding_box< C, REF_OF(V) > *  other,
bool  strict = true 
) [inherited]
bool is0D ( void  ) const [inline, inherited]

Definition at line 80 of file bounding_box.hpp.

{ return ((m_xmin == m_xmax) && (m_ymin == m_ymax) && (m_zmin == m_zmax)) ; }
bool is1D ( void  ) const [inline, inherited]

Definition at line 81 of file bounding_box.hpp.

{ return ((m_xmin != m_xmax) && (m_ymin == m_ymax) && (m_zmin == m_zmax)) ; }
bool is2D ( void  ) const [inline, inherited]

Definition at line 82 of file bounding_box.hpp.

{ return ((m_xmin != m_xmax) && (m_ymin != m_ymax) && (m_zmin == m_zmax)) ; }
bool is3d ( void  ) const [inline, inherited]

Definition at line 83 of file bounding_box.hpp.

{ return ((m_xmin != m_xmax) && (m_ymin != m_ymax) && (m_zmin != m_zmax)) ; }
bool is_active ( void  ) [virtual]

Implements cell< C, REF_OF(V) >.

Definition at line 1026 of file cell2d_voronoi_diagram.hpp.

                 {
  if ( this->is_bisector() ) 
  {
    return (this->m_objects[0])->is_active();
  }
  else
  {
    return true;
  }

}
bool is_border ( void  ) const [inline, inherited]

Definition at line 121 of file cell2d.hpp.

Referenced by voronoi2d< C, V >::run(), topology2d< C, V >::run(), semialgebraic2d< C, V >::run(), and arrangement2d< C, V >::run().

                                    {
      return (  this->s_neighbors.size()==0 ||
                this->e_neighbors.size()==0 ||
                this->n_neighbors.size()==0 ||
                this->w_neighbors.size()==0  );
  }
bool is_corner ( void  ) const [inherited]

Definition at line 431 of file cell2d.hpp.

Referenced by voronoi2d< C, V >::run(), semialgebraic2d< C, V >::run(), and arrangement2d< C, V >::run().

                      {

    if (this->s_neighbors.size()==0 &&
        this->e_neighbors.size()==0  )
        return true;
    else if (this->e_neighbors.size()==0 &&
             this->n_neighbors.size()==0 )
        return true;
    else if (this->n_neighbors.size()==0 &&
             this->w_neighbors.size()==0  )
        return true;
    else if (this->w_neighbors.size()==0 &&
             this->s_neighbors.size()==0 )
        return true;
    
    return false;
}
bool is_intersected ( void  ) [virtual]

Implements cell< C, REF_OF(V) >.

Definition at line 668 of file cell2d_voronoi_diagram.hpp.

                     {
  
  if(this->m_objects.size() >1 && !m_intersected) {
//      std::cout<<"Intersecting inside box "<< this <<std::endl;
      for(unsigned i=0; i<this->m_objects.size();i++)
          for(unsigned j=i+1; j<this->m_objects.size(); j++)
            Intersection2dFactory::instance()->compute(this->m_singular, (Shape*)this->m_objects[i], (Shape*)this->m_objects[j], (BoundingBox)*this);
      m_intersected = true;      
  }
  
  if (this->m_singular.size() > 0) return true;
  return false;
}
bool is_regular ( void  ) [virtual]

Implements cell< C, REF_OF(V) >.

Definition at line 654 of file cell2d_voronoi_diagram.hpp.

{
  //std::cout<<"bisector? "<< this->is_bisector()<<std::endl;
  if ( this->is_bisector() ) 
  {
    return (this->m_objects[0])->is_regular();
  }
  else
  {
    return false;
  }
}
virtual bool is_touching ( void  ) [inline, virtual]

Definition at line 78 of file cell2d_voronoi_diagram.hpp.

{return true; };
void join0 ( cell2d< C, V > *  b) [inline, inherited]

Definition at line 267 of file cell2d.hpp.

{
    this->e_neighbors << b; 
    b->w_neighbors << this; 
}
void join1 ( cell2d< C, V > *  b) [inline, inherited]

Definition at line 274 of file cell2d.hpp.

{
    b->s_neighbors << this;
    this->n_neighbors << b;
}
unsigned nb_intersect ( void  ) const [virtual]

Reimplemented from cell2d< C, V >.

Definition at line 1039 of file cell2d_voronoi_diagram.hpp.

References Cell2d.

                             {
    unsigned sum(0);
    Cell2d* c;
    foreach (Cell* m, m_objects)
    { 
        c = dynamic_cast<Cell2d*>(m);
        sum+= c->nb_intersect();
    }
    return sum;
  }
cell2d< C, V > * neighbor ( Point *  p) [virtual]

Reimplemented from cell2d< C, V >.

Definition at line 1140 of file cell2d_voronoi_diagram.hpp.

References Cell2d.

{
  foreach( Cell2d *c, this->s_neighbors     )
    if ( c->intersections(2).member(p) )
//    foreach( Point* q, c->intersections(2) )
//    if ( abs(p->x()-q->x())<EPSILON && abs(p->y()-q->y())<EPSILON )
      return c;

  foreach( Cell2d *c, this->e_neighbors     )
    if ( c->intersections(3).member(p) )
//    foreach( Point* q, c->intersections(3) )
//    if ( abs(p->x()-q->x())<EPSILON && abs(p->y()-q->y())<EPSILON )
      return c;

  foreach( Cell2d *c, this->n_neighbors     )
    if ( c->intersections(0).member(p) )
//    foreach( Point* q, c->intersections(0) )
//    if ( abs(p->x()-q->x())<EPSILON && abs(p->y()-q->y())<EPSILON )
      return c;

  foreach( Cell2d *c, this->w_neighbors     )
    if ( c->intersections(1).member(p) )
//    foreach( Point* q, c->intersections(1) )
//    if ( abs(p->x()-q->x())<EPSILON && abs(p->y()-q->y())<EPSILON )
      return c;
  
/*

  std::cout<<"Point "<<"("<<*p<<") not found in neighbs of "<< *this<<"( #neibs="<<this->neighbors().size() <<")"<<std::endl;

      foreach( Cell2d* c, this->neighbors() )
      {
        std::cout<< *c <<" ints:"<< ((SELF*)c)->intersections().size()  <<std::endl;
        foreach(Point* q, c->intersections() )
          std::cout<<"Point "<<q<<" ("<<*q<<")"<<std::endl;
      }
*/

    return NULL;
}
virtual Seq<cell2d *> neighbors ( ) [inline, virtual, inherited]

Definition at line 162 of file cell2d.hpp.

Referenced by voronoi2d< C, V >::run(), semialgebraic2d< C, V >::run(), and arrangement2d< C, V >::run().

                                       {
      Seq<cell2d *> r;
      r<< this->s_neighbors; 
      r<< this->e_neighbors; 
      r<< this->n_neighbors; 
      r<< this->w_neighbors;
  return ( r ); }
double& operator() ( unsigned  v,
unsigned  s 
) [inherited]
double operator() ( unsigned  v,
unsigned  s 
) const [inherited]
bounding_box<C,REF_OF(V) >* operator* ( const bounding_box< C, REF_OF(V) > &  other) [inline, inherited]

Definition at line 103 of file bounding_box.hpp.

{ return intersect(other) ; }
bounding_box<C,REF_OF(V) >* operator+ ( const bounding_box< C, REF_OF(V) > &  other) [inline, inherited]

Definition at line 104 of file bounding_box.hpp.

{ return     unite(other) ; }
cell2d_voronoi_diagram< C, V >::Point * pair ( Point *  p,
int &  sgn 
) [virtual]

Implements cell2d< C, V >.

Definition at line 1052 of file cell2d_voronoi_diagram.hpp.

References Cell2d.

{

//  std::cout<<(sgn>0?"+": "-")<<" pair of "<< *this<<"("<< p->x()<<","<<p->y()<<")"<<std::endl;

  if ( this->is_intersected() )  
  {
    //std::cout<<"Reached Vertex cell "<< *this << " ("<<sgn<<")"<<std::endl;
    //std::cout<<"sites are "<< this->m_sites <<std::endl;
    //foreach( Point* q, this->intersections() )
    //std::cout<< *q<<std::endl; 
  
    //Find bisector containing p
    
    unsigned st, cnt(0);
    foreach (Cell* mm, this->m_objects)
    { 
      Cell2d* m = dynamic_cast<Cell2d*>(mm);

      if ( m->intersections().member(p) )
//      foreach( Point* q, m->intersections() )
//        if ( abs(p->x()-q->x())<EPSILON && abs(p->y()-q->y())<EPSILON )
        { 
          // p found in bisector m.
          //std::cout<< "Current bisector: "<< cnt <<std::endl;
          // deduce site from sgn
          st=this->site(sgn,cnt);
          //std::cout<< "Site is: "<< st <<std::endl;
          // jump to a different bisector containing st
          unsigned cnt2(0);
          foreach (Cell* cc, this->m_objects)
          { 
            Cell2d* c = dynamic_cast<Cell2d*>(cc);
            if ( c!=m                   &&
               (st==this->site(1,cnt2)  ||
                st==this->site(-1,cnt2) ))
            {
              sgn= this->signof(st,cnt2);
//              std::cout<< "New bisector: "<< cnt2 <<std::endl;
//              std::cout<< "New sign: "<< sgn <<std::endl;
//              std::cout<< "start="<< *(c->starting_point(sgn))<<std::endl;
//              std::cout<< "end  ="<< *(c->pair(c->starting_point(sgn), sgn )) <<std::endl;

              return c->pair(c->starting_point(sgn), sgn );
            } 
            cnt2++;
          }
        }
      cnt++;
    }

  } else {
    
    Cell2d* c;
    foreach (Cell* m, m_objects)
    { 
      c = dynamic_cast<Cell2d*>(m);
      if ( c->intersections().member(p) )
//    foreach( Point* q, c->intersections() )
//      if ( abs(p->x()-q->x())<EPSILON && abs(p->y()-q->y())<EPSILON )
      { 
        //return c->pair(q,sgn);
        return c->pair(p,sgn);
      }
    }
  }
  std::cout<<"... Cell list pair trouble"<<std::endl;
  return NULL;
}
bool process_singular ( ) [virtual]

Definition at line 850 of file cell2d_voronoi_diagram.hpp.

References Cell2dAlgebraicCurve, and VSite.

                       {

//  std::cout<<"VD, Inserting singular"<<*this<<std::endl;  
//  ((voronoi2d<C,V>*)s)->m_singular_cells<< this; // does not work with forward declaration of voronoi2d
 
//  foreach( Point* q, this->intersections() )
//    std::cout<< *q<<"   adr  "<<q<<std::endl; 


     //CellList* l= new CellList( (BoundingBox)(*this) );
     Seq<Cell2dAlgebraicCurve*> l;
     Cell2dAlgebraicCurve* cc;

     //std::cout<<"compute arrangement of bisectors"<<std::endl;
     //More than one bisector in the cell: Compute arrangement
     Polynomial p;
     for ( unsigned i=0; i< this->m_objects.size(); i++ )
       for ( unsigned j=i+1; j< this->m_objects.size(); j++ )
       {
         p  = ((VSite*)(this->m_objects[i]))->m_polynomial ;
         p -= ((VSite*)(this->m_objects[j]))->m_polynomial ;
         
         cc= new Cell2dAlgebraicCurve( p,  (BoundingBox)(*this), false  );
         //if ( cc->is_active() ) //commented:Put all curves, even inactive!
           l<< cc;
       }

     this->m_objects.clear();
     this->m_objects<< l;
     this->is_intersected();
//     foreach(Cell * m, this->m_objects) m->insert_singular(s);

     return true;

     this->m_bisector=true;// .. 

     //foreach(Cell * m, l ) m->insert_singular(s);

     //if (this->m_singular.size()>0 ) 
     //  std::cout<<"VORONOI VERTEX COMPUTED in"<< *this <<std::endl;
   
}
void push_back ( cell< C, V > *  cv,
unsigned  k 
) [inline]

Definition at line 104 of file cell2d_voronoi_diagram.hpp.

References cell2d_voronoi_diagram< C, V >::m_objects, and cell2d_voronoi_diagram< C, V >::m_sites.

                                           {
       m_sites << k ; //object cv corresponds to site labeled k
       m_objects.push_back(cv); 
     };
void push_back ( cell< C, V > *  cv) [inline]

Definition at line 98 of file cell2d_voronoi_diagram.hpp.

References cell2d_voronoi_diagram< C, V >::m_objects, and cell2d_voronoi_diagram< C, V >::m_sites.

       {
         m_sites<< m_objects.size();
         m_objects.push_back(cv); 
       };
void push_bisector ( cell2d_algebraic_curve< C, V > *  cv,
Seq< unsigned >  k 
) [inline]

Definition at line 109 of file cell2d_voronoi_diagram.hpp.

References cell2d_voronoi_diagram< C, V >::m_objects, and cell2d_voronoi_diagram< C, V >::m_sites.

                                                                    {
       m_sites << k ; 
       m_objects.push_back(cv); 
     };
void set_xmax ( double  x) [inline, inherited]

Definition at line 74 of file bounding_box.hpp.

{ this->m_xmax = x ; }
void set_xmin ( double  x) [inline, inherited]

Definition at line 73 of file bounding_box.hpp.

{ this->m_xmin = x ; }
void set_ymax ( double  y) [inline, inherited]

Definition at line 76 of file bounding_box.hpp.

{ this->m_ymax = y ; }
void set_ymin ( double  y) [inline, inherited]

Definition at line 75 of file bounding_box.hpp.

{ this->m_ymin = y ; }
void set_zmax ( double  z) [inline, inherited]

Definition at line 78 of file bounding_box.hpp.

{ this->m_zmax = z ; }
void set_zmin ( double  z) [inline, inherited]

Definition at line 77 of file bounding_box.hpp.

{ this->m_zmin = z ; }
int side ( Point *  p) [inline, inherited]

Definition at line 140 of file cell2d.hpp.

                       {
      Seq<Point*> all;
      int s,i,a;
      s   = s_intersections.size();
      all = this->intersections();
      a   = all.size();
      i   = all.search(p);
      if (i==-1) return (-1);
      else return
         ( i<s                             ? 0 :
         ( i<s+(int)e_intersections.size() ? 1 :
         ( i<a-(int)w_intersections.size() ? 2 :
                                      3 )));
  }
int signature ( int &  i,
int &  j 
) [inline]

Definition at line 120 of file cell2d_voronoi_diagram.hpp.

References cell2d_voronoi_diagram< C, V >::m_sites.

                                            {
       int c(0);
       for ( int u=0; u<i; u++)
         for ( int v=u+1; v<m_sites.size(); v++)
           c++;
       return c + j-i-1; }
int signof ( unsigned  st,
unsigned  bs = 0 
) [inline]

Definition at line 141 of file cell2d_voronoi_diagram.hpp.

References cell2d_voronoi_diagram< C, V >::count(), cell2d_voronoi_diagram< C, V >::m_objects, and cell2d_voronoi_diagram< C, V >::m_sites.

                                            {

       if (this->m_objects.size()==1 )
         return ( st==m_sites[0]? -1 :1 ); 

       //std::cout<<"Sgnof " <<st<<"(bs="<<bs<<") on "<< *this<<"objs="<<this->m_objects.size()<<std::endl;

       unsigned n=this->count() - 1;
       unsigned i,j(0),k(0);

       for (i=0;i<=bs;i++)
         if ( k<n )
           k++ ;
         else
           j++ ;

       if (st==this->m_sites[j])   return (-1);
       if (st==this->m_sites[k])   return (1);

       std::cout<<"problem at \"signof\" "<<i <<", "<< *this <<"sites= "<<m_sites<<std::endl;
       return 0;
     };
unsigned site ( int  sgn,
unsigned  bs = 0 
) [inline]

Definition at line 127 of file cell2d_voronoi_diagram.hpp.

References cell2d_voronoi_diagram< C, V >::count(), and cell2d_voronoi_diagram< C, V >::m_sites.

                                           { 
       unsigned n=this->count();
       unsigned i,k(bs+1);
       
       for (i=1;i<n;i++)
         if ( k>n-i )
           k-= n-i;
         else
           break;
       
       //return( sgn>0 ? m_sites[i-1+k]: m_sites[i-1])  ; 
       return ( m_sites[i-1 + (sgn>0?k:0)] )  ; 
     }
Seq<unsigned> sites ( ) const [inline]

Definition at line 164 of file cell2d_voronoi_diagram.hpp.

References cell2d_voronoi_diagram< C, V >::m_sites.

{ return m_sites;};
double size ( void  ) [inherited]
void split_position ( int &  v,
double &  t 
) [virtual]

Reimplemented from cell2d< C, V >.

Definition at line 894 of file cell2d_voronoi_diagram.hpp.

                                      {
  double sx = (this->xmax()-this->xmin());
  double sy = (this->ymax()-this->ymin());
  if(sx<sy) {
    v=1;
    s=(this->ymax()+this->ymin())/2;
  } else {
    v=0;
    s=(this->xmax()+this->xmin())/2;
  }
}
cell2d_voronoi_diagram< C, V >::Point * starting_point ( int  sgn) [virtual]

Implements cell2d< C, V >.

Definition at line 1123 of file cell2d_voronoi_diagram.hpp.

References Cell2d, cell< C, V >::is_active(), and VSite.

{
//  std::cout<<"starting point(voronoi diagram)"<<std::endl;

   Cell2d* c;
   foreach (Cell* m, m_objects)
    { 
        if ( m->is_active() )
        {
            c = dynamic_cast<Cell2d*>(m);           
            return ((VSite*)c)->starting_point(sgn);
        }
    }
    return NULL; 
}
void subdivide ( cell< C, V > *&  left,
cell< C, V > *&  right,
int  v,
double  s 
) [virtual]

Definition at line 907 of file cell2d_voronoi_diagram.hpp.

References Cell2dAlgebraicCurve, mmx::shape_ssi::left(), mmx::shape_ssi::right(), SELF, cell< C, V >::subdivide(), mmx::shape::upper(), VSite, point< C, V, N >::x(), and point< C, V, N >::y().

                                                             {

  //std::cout<<"Subdividing "<< this << "sites="<<this->m_sites <<std::endl;

  typedef SELF Cell_t;

  if(v==1) {
    left =(Cell*)new Cell_t(this->xmin(), this->xmax(), this->ymin(), c, m_intersected) ;
    right=(Cell*)new Cell_t(this->xmin(), this->xmax(), c, this->ymax(), m_intersected) ;
    
    foreach(Point * p, this->m_singular) {
      if(p->y() <=  c) 
        ((Cell_t*) left)->m_singular << p ;
      else
        ((Cell_t*)right)->m_singular << p ;
    }

    /*  Update neighbors  */
    this->connect1( (Cell_t*)left, (Cell_t*)right);
    ((Cell_t*)left)->join1((Cell_t*)right);

  } else {//v==0
    left = (Cell*)new Cell_t(this->xmin(), c, this->ymin(), this->ymax(), m_intersected) ;
    right= (Cell*)new Cell_t(c, this->xmax(), this->ymin(), this->ymax(), m_intersected) ;

    foreach(Point * p, this->m_singular) {
      if(p->x() <= c ) 
        ((Cell_t*)left)->m_singular << p ;
      else
        ((Cell_t*)right)->m_singular << p ;
    }

    /*  Update neighbors  */
    this->connect0((Cell_t*)left, (Cell_t*)right);
    ((Cell_t*)left)->join0((Cell_t*)right);

  }

  /* disconnect parent */
  this->disconnect( );

  if (!this->is_bisector() ) 
  {

  Seq<VSite*> ll, rr;
  Cell * cv_left, * cv_right;

  foreach(Cell* cv, this->m_objects) {
    cv->subdivide( cv_left, cv_right);
      ll<< (VSite*)cv_left;
      rr<< (VSite*)cv_right;
  }

  /* Filtering sites that are "far away" */
  //1. find minimum upper bound 
  //2. remove all cells whose lower bound is bigger than that
  //std::cout<<"Filtering Cells "<< cv_left<<" , "<<cv_right<<std::endl;

  /* Left cell */
  double mm;
  unsigned cnt;
  mm=  ( (VSite*)ll.min(this->comp_up) )->upper();
  
  cnt=0;
  foreach(VSite* vs, ll)
  {
    //std::cout<<"check "<< m_sites[cnt]<<std::endl;
    if ( !this->over(vs,mm) )
    {
      ((Cell_t*)left)->push_back( vs, m_sites[cnt] );
      //std::cout<<"added "<< m_sites[cnt]<<std::endl;
    }
    cnt++;
    //else
    //{
    //delete vs;
    //ll.erase( ll.search(vs) ) ;
    //}
  }

  /* Right cell */
  mm=  ( (VSite*)rr.min(this->comp_up) )->upper();
  
  cnt=0;
  foreach(VSite* vs, rr)
  {
    if ( !this->over(vs,mm) )
    {
      ((Cell_t*)right)->push_back( vs, m_sites[cnt] );
      //((Cell_t*)right)->m_objects<< (Cell*)vs;
    }
    //else
    //{
    //delete vs;
    //ll.erase( ll.search(vs) ) ;
    //}
    cnt++;
  }
  }
  else
  {//bisector box

    Cell * cv_left, * cv_right;
    //std::cout<<"bisector subdiv " <<std::endl;
    this->m_objects[0]->subdivide( cv_left, cv_right);
    ((Cell_t*)left)->push_bisector( (Cell2dAlgebraicCurve*)cv_left,  m_sites );
    ((Cell_t*)right)->push_bisector((Cell2dAlgebraicCurve*)cv_right, m_sites );

    ((Cell_t*)left)->m_bisector=true;
    ((Cell_t*)right)->m_bisector=true;
    
  }

//    std::cout<<"ok " <<std::endl;  
}
virtual void subdivide ( cell< C, REF_OF(V) > *&  left,
cell< C, REF_OF(V) > *&  right,
int  v,
double  s 
) [pure virtual, inherited]
virtual int subdivide ( cell< C, REF_OF(V) > *&  left,
cell< C, REF_OF(V) > *&  right 
) [virtual, inherited]
bounding_box<C,REF_OF(V) >* unite ( bounding_box< C, REF_OF(V) > *  other) [inherited]
void united ( bounding_box< C, REF_OF(V) > *  other) [inherited]
bool unites ( bounding_box< C, REF_OF(V) > *  other,
bool  strict = true 
) [inherited]
double xmax ( void  ) [inline, inherited]

Definition at line 56 of file bounding_box.hpp.

Referenced by cell2d_voronoi_diagram< C, V >::compute_boundary().

{ return m_xmax ; }
double xmax ( void  ) const [inline, inherited]

Definition at line 63 of file bounding_box.hpp.

{ return m_xmax ; }
double xmin ( void  ) [inline, inherited]

Definition at line 55 of file bounding_box.hpp.

Referenced by cell2d_voronoi_diagram< C, V >::compute_boundary().

{ return m_xmin ; }
double xmin ( void  ) const [inline, inherited]

Definition at line 62 of file bounding_box.hpp.

{ return m_xmin ; }
double xsize ( void  ) const [inline, inherited]

Definition at line 69 of file bounding_box.hpp.

{ return m_xmax-m_xmin ; }
double ymax ( void  ) const [inline, inherited]

Definition at line 65 of file bounding_box.hpp.

{ return m_ymax ; }
double ymax ( void  ) [inline, inherited]

Definition at line 58 of file bounding_box.hpp.

Referenced by cell2d_voronoi_diagram< C, V >::compute_boundary().

{ return m_ymax ; }
double ymin ( void  ) const [inline, inherited]

Definition at line 64 of file bounding_box.hpp.

{ return m_ymin ; }
double ymin ( void  ) [inline, inherited]

Definition at line 57 of file bounding_box.hpp.

Referenced by cell2d_voronoi_diagram< C, V >::compute_boundary().

{ return m_ymin ; }
double ysize ( void  ) const [inline, inherited]

Definition at line 70 of file bounding_box.hpp.

{ return m_ymax-m_ymin ; }
double zmax ( void  ) const [inline, inherited]

Definition at line 67 of file bounding_box.hpp.

{ return m_zmax ; }
double zmax ( void  ) [inline, inherited]

Definition at line 60 of file bounding_box.hpp.

{ return m_zmax ; }
double zmin ( void  ) [inline, inherited]

Definition at line 59 of file bounding_box.hpp.

{ return m_zmin ; }
double zmin ( void  ) const [inline, inherited]

Definition at line 66 of file bounding_box.hpp.

{ return m_zmin ; }
double zsize ( void  ) const [inline, inherited]

Definition at line 71 of file bounding_box.hpp.

{ return m_zmax-m_zmin ; }

Member Data Documentation

Seq<Point *> e_intersections [inherited]

Definition at line 130 of file cell2d.hpp.

Referenced by cell2d< C, REF_OF(V) >::intersections(), cell2d< C, REF_OF(V) >::nb_intersect(), cell2d< C, REF_OF(V) >::neighbor(), and cell2d< C, REF_OF(V) >::side().

Seq<cell2d *> e_neighbors [inherited]

Definition at line 171 of file cell2d.hpp.

Referenced by cell2d_voronoi_diagram< C, V >::compute_boundary(), cell2d< C, REF_OF(V) >::is_border(), cell2d< C, REF_OF(V) >::neighbor(), cell2d< C, REF_OF(V) >::neighbors(), voronoi2d< C, V >::run(), topology2d< C, V >::run(), semialgebraic2d< C, V >::run(), and arrangement2d< C, V >::run().

bool m_bisector [protected]

Definition at line 174 of file cell2d_voronoi_diagram.hpp.

Referenced by cell2d_voronoi_diagram< C, V >::compute_boundary().

gNode<cell2d*>* m_gnode [inherited]

Definition at line 138 of file cell2d.hpp.

Referenced by voronoi2d< C, V >::run(), and topology2d< C, V >::run().

bool m_intersected [protected]

Definition at line 173 of file cell2d_voronoi_diagram.hpp.

Seq< cell<C,V> *> m_objects

Definition at line 165 of file cell2d_voronoi_diagram.hpp.

Referenced by cell2d_voronoi_diagram< C, V >::compute_boundary(), cell2d_voronoi_diagram< C, V >::count(), cell2d_voronoi_diagram< C, V >::func(), cell2d_voronoi_diagram< C, V >::intersections(), cell2d_voronoi_diagram< C, V >::push_back(), cell2d_voronoi_diagram< C, V >::push_bisector(), and cell2d_voronoi_diagram< C, V >::signof().

Seq<Point *> m_singular [inherited]

Definition at line 133 of file cell2d.hpp.

Seq<unsigned> m_sites [protected]

Definition at line 172 of file cell2d_voronoi_diagram.hpp.

Referenced by cell2d_voronoi_diagram< C, V >::compute_boundary(), cell2d_voronoi_diagram< C, V >::push_back(), cell2d_voronoi_diagram< C, V >::push_bisector(), cell2d_voronoi_diagram< C, V >::signature(), cell2d_voronoi_diagram< C, V >::signof(), cell2d_voronoi_diagram< C, V >::site(), and cell2d_voronoi_diagram< C, V >::sites().

bool m_treated [protected]

Definition at line 175 of file cell2d_voronoi_diagram.hpp.

Referenced by cell2d_voronoi_diagram< C, V >::compute_boundary().

double m_xmax [protected, inherited]

Definition at line 107 of file bounding_box.hpp.

double m_xmin [protected, inherited]

Definition at line 107 of file bounding_box.hpp.

double m_ymax [protected, inherited]

Definition at line 108 of file bounding_box.hpp.

double m_ymin [protected, inherited]

Definition at line 108 of file bounding_box.hpp.

double m_zmax [protected, inherited]

Definition at line 109 of file bounding_box.hpp.

double m_zmin [protected, inherited]

Definition at line 109 of file bounding_box.hpp.

Seq<Point *> n_intersections [inherited]

Definition at line 131 of file cell2d.hpp.

Referenced by cell2d< C, REF_OF(V) >::intersections(), cell2d< C, REF_OF(V) >::nb_intersect(), and cell2d< C, REF_OF(V) >::neighbor().

Seq<cell2d *> n_neighbors [inherited]

Definition at line 172 of file cell2d.hpp.

Referenced by cell2d_voronoi_diagram< C, V >::compute_boundary(), cell2d< C, REF_OF(V) >::is_border(), cell2d< C, REF_OF(V) >::neighbor(), cell2d< C, REF_OF(V) >::neighbors(), voronoi2d< C, V >::run(), topology2d< C, V >::run(), semialgebraic2d< C, V >::run(), and arrangement2d< C, V >::run().

Seq<Point *> s_intersections [inherited]

Definition at line 129 of file cell2d.hpp.

Referenced by cell2d< C, REF_OF(V) >::intersections(), cell2d< C, REF_OF(V) >::nb_intersect(), cell2d< C, REF_OF(V) >::neighbor(), and cell2d< C, REF_OF(V) >::side().

Seq<cell2d *> s_neighbors [inherited]

Definition at line 170 of file cell2d.hpp.

Referenced by cell2d_voronoi_diagram< C, V >::compute_boundary(), cell2d< C, REF_OF(V) >::is_border(), cell2d< C, REF_OF(V) >::neighbor(), cell2d< C, REF_OF(V) >::neighbors(), voronoi2d< C, V >::run(), topology2d< C, V >::run(), semialgebraic2d< C, V >::run(), and arrangement2d< C, V >::run().

Seq<Point *> w_intersections [inherited]

Definition at line 132 of file cell2d.hpp.

Referenced by cell2d< C, REF_OF(V) >::intersections(), cell2d< C, REF_OF(V) >::nb_intersect(), cell2d< C, REF_OF(V) >::neighbor(), and cell2d< C, REF_OF(V) >::side().

Seq<cell2d *> w_neighbors [inherited]

Definition at line 173 of file cell2d.hpp.

Referenced by cell2d_voronoi_diagram< C, V >::compute_boundary(), cell2d< C, REF_OF(V) >::is_border(), cell2d< C, REF_OF(V) >::neighbor(), cell2d< C, REF_OF(V) >::neighbors(), voronoi2d< C, V >::run(), topology2d< C, V >::run(), semialgebraic2d< C, V >::run(), and arrangement2d< C, V >::run().

The documentation for this class was generated from the following file: