realroot_doc 0.1.1
Classes | Functions
mmx::univariate Namespace Reference

Module for Univariate POLynomials with a Direct Access Representation. More...

Classes

Functions

Detailed Description

Module for Univariate POLynomials with a Direct Access Representation.

It contains generic implementations on univariate (dense) polynomials. This set of functions apply when R provides the following methods or definitions: 

       typename R::value_type;
       typename R::size_type;
       typename R::iterator;
       typename R::reverse_iterator;
       
       iterator_t R::begin();
       iterator_t R::end();
       value_type R::operator[](int);

Function Documentation

void mmx::univariate::add ( monomials< C > &  r,
const monomials< C > &  a,
const monomials< C > &  b 
) [inline]

Definition at line 216 of file univariate.hpp.

References check_degree().

Referenced by use< operators_of, univariate::monomials< C > >::add(), add(), and div_rem().

                                                                {
    array::add(r,a,b);
    check_degree(r);
  }
void mmx::univariate::add ( monomials< C > &  r,
const monomials< C > &  a,
const C &  c 
) [inline]

Definition at line 223 of file univariate.hpp.

References check_degree(), degree(), and Polynomial.

                                                      {
    if(degree(a)>-1) {
      r=a; r[0]+=c;
    }
    else
      r= Polynomial(c,0);
    check_degree(r);
  }
void mmx::univariate::add ( monomials< C > &  r,
const C &  c 
) [inline]

Definition at line 234 of file univariate.hpp.

References check_degree(), degree(), and Polynomial.

                                 {
    if(degree(r)>-1) {
     r[0]+=c;
    }
    else
      r= Polynomial(c,0);
    check_degree(r);
  }
void mmx::univariate::add ( monomials< C > &  r,
const monomials< C > &  a 
) [inline]

Definition at line 244 of file univariate.hpp.

References add(), and check_degree().

                                          {
    array::add(r,a);
    check_degree(r);
  }
void mmx::univariate::add_cst ( R &  r,
const S &  c 
) [inline]

Definition at line 429 of file univariate.hpp.

{ r[0]+=c; }
int mmx::univariate::check_degree ( monomials< C > &  a) [inline]

Definition at line 207 of file univariate.hpp.

Referenced by add(), div(), monomials< C >::monomials(), mul(), and sub().

                              {
    int l = a.degree_;
    while(l >=0 && (a.tab_[l]==0)) {l--;}
    a.degree_=l;
    return a.degree_;
  }
void mmx::univariate::checkdegree ( R &  p) [inline]

Definition at line 579 of file univariate.hpp.

Referenced by set_monomial().

                                                 { 
  int d = p.size()-1; 
  if ( d < 0 ) return;
  while ( p[d] == 0 ) d--;
  p.resize(d+1);
}
void mmx::univariate::coeff_modulo ( R &  r,
const typename R::value_type &  x 
)

Definition at line 873 of file univariate.hpp.

                                                           {
  for ( typename R::iterator i = r.begin(); i != r.end(); *i %= x, ++i ) ;
};
void mmx::univariate::convertm2b ( T &  bz,
const P &  p,
unsigned  size,
const C &  a,
const C &  b 
)

Convert the representation in the monomial basis to the representation in the Bezier basis of $[a,b]$. The matrix of the change of bases is $(c_{i,j})_{0 i,j d}$ with $c_{i,j}= {{i}{j}}/{{d}{j}}$ if $j i$ and $0$ otherwise.

Definition at line 847 of file univariate.hpp.

References mmx::assign(), scale(), mmx::array::set_cst(), shift(), and mmx::size().

Referenced by binary_sleeve_subdivision< K >::init_pol().

                                                                     {
  typedef typename T::value_type coeff_t;
  T pps(p.size());
  array::assign(pps,p);
  
  if(a !=0)
    shift(pps,pps,a);
  
  scale(pps, pps, C(b-a));
  
  array::set_cst(bz,pps[0]);
  int dn=1, nm=1;
  
  for(unsigned j=1; j<size; j++) {
    dn *= (size-j); dn/= j;
    nm=1;
    bz[j] += pps[j]/dn;
    for(unsigned i=j+1; i<size; i++) {
      nm *= i; nm/= (i-j);
      bz[i] += pps[j]*nm/dn;
    }
  }
}
int mmx::univariate::degree ( const monomials< C > &  a) [inline]

Definition at line 201 of file univariate.hpp.

{ return a.degree_;}
int mmx::univariate::degree ( const R &  p)

Definition at line 194 of file univariate.hpp.

Referenced by add(), diff(), div_rem(), eval_homogeneous(), eval_horner(), eval_horner_idx(), lcoeff(), mmx::min_bound(), mul(), mul_index(), numer(), monomials< C >::operator==(), print(), reciprocal(), shift(), and sub().

                          {
    // std::cout <<"(Using default degree) "<<p<<std::endl;
    int i = p.size()-1;
    while(i>-1 && p[i]==(typename R::value_type)0) i--;
    return i;
  }
R::value_type mmx::univariate::derive ( const R  p,
typename R::value_type  x 
)
R::value_type mmx::univariate::derive ( const R &  Pol,
const typename R::value_type &  x 
) [inline]

Return an evaluation of the derivation of an univariate polynomial for the value 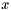$x$. Example: 

    upoldse<R> p(...);
    upoldse<R>::value_type x,d;
    d=univariate::derive(p,x);

Definition at line 755 of file univariate.hpp.

References eval().

{ 
  typename R::value_type p,res;
  eval(p,res,Pol,x); 
  return res;
};
R diff ( const R &  p) [inline]

The derivative of the polynomial p is put in r.

Definition at line 630 of file univariate.hpp.

{
  R r(p); 
  diff(r,p);
  return r;
}
void mmx::univariate::diff ( R &  r,
const R &  p 
) [inline]

The derivative of the polynomial p is put in r. r should be allocated wi the correct size.

Definition at line 608 of file univariate.hpp.

References degree().

{
  int n,i;
  r.resize(n=degree(p));
  for( i = 1; i < n+1; ++i) r[i-1] =p[i]*i;
}
void mmx::univariate::div ( monomials< C > &  r,
const monomials< C > &  a,
const monomials< C > &  b 
) [inline]

Definition at line 330 of file univariate.hpp.

References assert, check_degree(), div_rem(), and Polynomial.

Referenced by use< operators_of, univariate::monomials< C > >::div().

                                                                {
    assert(&r!=&a);
    Polynomial tmp(a);
    r = Polynomial(0);
    div_rem(r,tmp,b);
    check_degree(r);
  }
void mmx::univariate::div ( monomials< C > &  r,
const monomials< C > &  b 
) [inline]

Definition at line 340 of file univariate.hpp.

References check_degree(), div_rem(), and Polynomial.

                                          {
    Polynomial tmp(r);
    r = Polynomial(0);
    div_rem(r,tmp,b);
    check_degree(r);
  }
void mmx::univariate::div ( monomials< C > &  r,
const C &  c 
) [inline]

Definition at line 349 of file univariate.hpp.

References check_degree(), and mmx::array::div_ext().

                                  {
    array::div_ext(r,c);
    check_degree(r);
  }
void mmx::univariate::div_rem ( R &  q,
R &  a,
const R &  b 
)

Quotient and remainder of a by b. The polynomial a is modified. At the end of the computation, it is equal to the remainder in the euclidean division. The type R should provide a degree function and a direct access operator.

Definition at line 559 of file univariate.hpp.

References add(), degree(), mul(), and sub().

Referenced by div().

  {
    typedef typename R::iterator iterator;
    int da = degree(a), db=degree(b);
    typename R::value_type lb=b[db];
    R t;
    q=(R)0;
    while (da>=db) {
      while(a[da]==0 && da>=db) da--;
      if(da>=db) {
        R m( a[da]/lb, da-db );
        mul(t,b,m);
        t[da]=a[da];
        sub(a,t);
        add(q,m);
      }
    }
  }
C mmx::univariate::eval ( const R &  p,
const C &  c 
) [inline]

Definition at line 520 of file univariate.hpp.

References eval_horner().

Referenced by derive().

  {
    return eval_horner(p,c);
  }
void mmx::univariate::eval ( O &  p,
O &  dp,
const R &  Pol,
const I &  x 
) [inline]

Return an evaluation of the polynomial and its derivative at 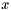$x$ Example: 

    upoldse<R> p(...);
    upoldse<R>::value_type x,vp,vd;
    d=univariate::eval(vp,vd,p,x);

Definition at line 738 of file univariate.hpp.

{
  int n = p.size()-1;
  p  = Pol[n];
  dp = O(0);
  for ( int j = n-1; j >= 0; dp = dp*x + p, p =p*x + Pol[j], j-- ) ; 
};
C mmx::univariate::eval_homogeneous ( const R &  p,
const C &  a,
const C &  b 
) [inline]

Definition at line 526 of file univariate.hpp.

References mmx::assign(), and degree().

Referenced by mmx::as_interval_data().

  {
    using namespace let;
    C r,y=1,cf;
    if(degree(p)>0) {
      typedef typename R::const_reverse_iterator const_reverse_iterator;
      const_reverse_iterator it=p.rbegin();
      assign(r,*it); it++;
      //        for(; it !=p.rend(); ++it) {r*=c; assign(cf,*it); r+=cf;}
      for(; it !=p.rend(); ++it) {r*=a; y *=b; assign(cf,*it); r=r+cf*y;}
      return r;
    } else if(degree(p)==0)
      {
        assign(r,p[0]); return r;
      }
    else
      return C(0);
  }
C mmx::univariate::eval_horner ( const R &  p,
const C &  c 
) [inline]

Definition at line 486 of file univariate.hpp.

References mmx::assign(), and degree().

Referenced by eval(), and sign_at().

  {
    using namespace let;
    C r,cf;
    if(degree(p)>0) {
      typedef typename R::const_reverse_iterator const_reverse_iterator;
      const_reverse_iterator it=p.rbegin();
        assign(r,*it); it++;
        //      for(; it !=p.rend(); ++it) {r*=c; assign(cf,*it); r+=cf;}
        for(; it !=p.rend(); ++it) {r=r*c; assign(cf,*it); r=r+cf;}
        return r;
    } else if(degree(p)>-1)
      {
        assign(r,p[0]); return r;
      }
    else
      return C(0);
  }
C mmx::univariate::eval_horner_idx ( const R &  p,
const C &  c 
) [inline]

Definition at line 506 of file univariate.hpp.

References degree().

  {
    if(degree(p)>0) {
      int d=degree(p);
      C r=p[d];
      for(int i=d-1; i>-1; --i) {r*=c; r+= p[i];}
      return r;
    } else if(degree(p)>-1)
      return p[0];
    else
      return C(0);
  }
void mmx::univariate::inv_scale ( R &  r,
const R &  p,
const C &  l 
)

Scale the variable in the polynomial p by l and put the result r. It computes the coefficients of the polynomial 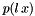$p(l \, x)$.

Definition at line 828 of file univariate.hpp.

Referenced by mmx::inv_scale().

{
  int sz=p.size();
  r.resize(sz);
  sz--;
  r[sz]=p[sz];
  typename R::value_type s=l;
  for(int i=sz-1; i>=0;i--){
    r[i]=p[i]*s;
    s *=l;
  }
}
R::value_type mmx::univariate::lcoeff ( const R &  p) [inline]

Returns the leading coefficient of the polynomial p.

Definition at line 357 of file univariate.hpp.

References degree().

Referenced by Cauchy< C >::upper_bound().

                     {
    return p[degree(p)];
  }
void mmx::univariate::mul ( R &  a,
const R &  b 
) [inline]

Definition at line 463 of file univariate.hpp.

References degree(), mul_index(), and mmx::array::set_cst().

  {
    if(degree(a)>=0 && degree(b)>=0)
      {
        R ta(a);
        a.resize(degree(a)+degree(b)+1);
        array::set_cst(a,0);
        mul_index(a,ta,b);
      }
    else
      array::set_cst(a,0);
  }
void mmx::univariate::mul ( monomials< C > &  r,
const monomials< C > &  p,
const C &  c 
) [inline]

Definition at line 311 of file univariate.hpp.

References check_degree(), and mul().

                                                       {
    r=p; mul(r,c); check_degree(r);
  }
void mmx::univariate::mul ( monomials< C > &  r,
const monomials< C > &  a,
const monomials< C > &  b 
) [inline]

Definition at line 287 of file univariate.hpp.

References assert, check_degree(), degree(), mmx::vctops::max(), mul_index(), and mmx::array::set_cst().

Referenced by div_rem(), use< operators_of, univariate::monomials< C > >::mul(), and mul().

                                                                {
    assert(&r!=&a);
    
    r.resize(std::max(degree(a)+degree(b)+1,0));
    array::set_cst(r,(C)0);
    mul_index(r,a,b);
    check_degree(r);
  }
void mmx::univariate::mul ( monomials< C > &  r,
const C &  c 
) [inline]

Multiplication of a polynomial by a monomial or a scalar.

Definition at line 299 of file univariate.hpp.

References mmx::array::mul_ext().

                                  {
    array::mul_ext(r,c);
  }
void mmx::univariate::mul ( monomials< C > &  a,
const monomials< C > &  b 
) [inline]

Multiplication of a polynomial by a polynomial;.

Definition at line 306 of file univariate.hpp.

References mul(), and Polynomial.

                                           {
    Polynomial r; mul(r,a,b); a=r;
  }
void mmx::univariate::mul_index ( R &  a,
const R &  b 
) [inline]

Definition at line 477 of file univariate.hpp.

References degree(), mul_index(), and mmx::array::set_cst().

  {
    R ta(a);
    a.resize(degree(a)+degree(b)+1);
    array::set_cst(a,0);
    mul_index(a,ta,b);
  }
void mmx::univariate::mul_index ( R &  r,
const R &  a,
const R &  b 
) [inline]

Definition at line 435 of file univariate.hpp.

References degree(), and Scalar.

Referenced by mul(), and mul_index().

  {
    typedef typename R::coeff_t Scalar;
    int da=degree(a), db=degree(b),i,j;
    for (i=0;i<=db;i++) {
      if  (b[i] == 0) continue;
      for (j=0;j<=da;j++) r[i+j] += a[j]*b[i];
    }
  }
void mmx::univariate::mul_index_it ( R &  r,
const R &  a,
const R &  b 
) [inline]

Definition at line 446 of file univariate.hpp.

  {
    typename R::const_iterator ia, ib;
    typename R::iterator       ir, it;
    ir=r.begin();
    for (ib=b.begin();ib !=b.end()&& ir != r.end();++ib) {
      typename R::value_type c = *ib;
      it=ir;
      if  (c==0) {++ir;continue;}
      for (ia=a.begin();ia!=a.end();++ia,++it) {
        (*it)+=(*ia)*c;
      }
      ++ir;
    }
  }
S mmx::univariate::numer ( const R &  f)

Definition at line 878 of file univariate.hpp.

References degree(), mmx::denominator(), mmx::lcm(), and mmx::numerator().

                     {
  S p(0,degree(f));
  typename S::value_type d=1;
  for(int i=0;i<degree(f)+1;i++) {
    if (f[i] !=0) d=lcm(d,denominator(f[i]));
  }
  for(int i=0;i<degree(f)+1;i++) 
    p[i]=numerator(f[i])* (d/denominator(f[i]));
  return p;
}
OSTREAM& mmx::univariate::print ( OSTREAM &  os,
const monomials< C > &  p,
const VAR &  var 
) [inline]

Definition at line 376 of file univariate.hpp.

References degree(), and print_as_coeff().

Referenced by print().

  {
    typedef typename Polynomial::value_type coeff_t;
    bool plus=false, not_one;
    if ( degree(p)<0) 
      os << coeff_t(0) ;
    else {
      for(int i= 0; i<=degree(p); i++)
      {
        if(p[i]!= (coeff_t)0) 
        {
          not_one = (p[i] != (coeff_t)1);
          if(not_one || i==0)
            print_as_coeff(os,p[i],plus);
          plus=true;
          //      if(i != degree(p) && with_plus_sign(p[i])) os<<"+"; 
          if(i>0)
            {
              //              if(p[i] == (coeff_t)(-1)) os<<"-";
              //              else 
              if(not_one) 
                os<<"*";
              os<<"x";
              if(i !=1) 
                {os<<'^'; os<<i;}
            }
//        else
//            os<<p[0];
        }
      }
      if(!plus) os << 0 ;
    }
    return os;
  }
OSTREAM& mmx::univariate::print ( OSTREAM &  os,
const monomials< C > &  p 
) [inline]

Definition at line 412 of file univariate.hpp.

References print().

                                          {
    return print(os,p, "x");
  }
OSTREAM& mmx::univariate::print_as_coeff ( OSTREAM &  os,
const C &  c,
bool  plus 
)

Definition at line 367 of file univariate.hpp.

Referenced by print().

  {
    if(plus) 
      os <<"+";
    os<<"("<<c<<")";
    return os;
  }
void reciprocal ( R &  w,
const R &  p 
)

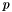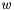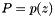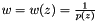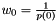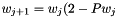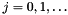Compute the reciprocal of the univariate polynomial $p$. The result is given in $w$. We assume $p[0] != 0$. For this, we consider the equation $f(w)\ =\ P - \frac{1}{w}\ =\ 0$, where $P=p(z)$, $w=w(z)= \frac{1}{p(z)}$ over the ring of formal power series in $z$, and apply Newton's iteration to this equation. So we have : $w_{0}=\frac{1}{p(0)}$, and $w_{j+1}=w_{j}(2-Pw_{j}$ where $j=0,1,\ldots$ By reducing the different polynomials modulo 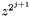$z^{2^{j+1}}$ at each step, we have two convolutions of two pairs of vectors of dimensions at most 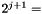$2^{j+1}=$ by step.

Definition at line 660 of file univariate.hpp.

References degree(), mmx::log(), mmx::pow(), and reduce().

{
  typedef typename R::size_type size_type;
  typedef typename R::value_type C;

  const size_type deg = univariate::degree(p)+1;
  R w0(deg),v(deg),xp(p);
  size_type K = (size_type) (std::log(p.degree()+1)/std::log(2)),j=1;
  C p0 = xp[deg-1];

  xp /= p0;
  w0 =xp/xp[0];
  v = w0;
  v *= C(-1.0);
  v[0]+=C(2);
  w=v/xp[0];
  w0=w;
  while (j <= K) {
    univariate::reduce(w0,pow(2,j+1));
    w=xp*w0;
    v =w;
    v*=C(-1.0);
    v[0]+=C(2);
    univariate::reduce(v,pow(2,j+1));
    w=w0*v;
    w0=w;
    j++;
  }
   univariate::reduce(w,deg);
   w/=p0;
}
void mmx::univariate::reduce ( T &  p,
const typename T::size_type &  e 
) [inline]

Truncate an univariate polynomial 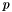$p$ which is modified in output, with a new degree of $e-1$.

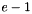Definition at line 696 of file univariate.hpp.

{
  // il me semble que tout ca c'est la meme chose que p.resize(e) 
  T temp(e);
  for (typename T::size_type i = 0; i < e; i++) temp[i]=p[i];
  p.resize(e);
  //  p.degree()=e-1;
  for (typename T::size_type i = 0; i < e; i++) p[i]=temp[i];
}
void mmx::univariate::reduce ( R &  p,
const typename R::size_type &  e 
)

Referenced by reciprocal(), and subdivisor< CELL, V >::run().

void mmx::univariate::reverse ( R &  p,
typename R::size_type  n 
)

Definition at line 590 of file univariate.hpp.

References mmx::sparse::swap().

Referenced by mmx::min_bound().

{
  int l=n-1;
  for(typename R::size_type i=0;i<n/2;i++) 
    std::swap(p[i],p[l-i]);
}
void mmx::univariate::reverse ( T &  p,
int  n 
) [inline]

Reverse the coefficients of an univariate polynomial, it is performed in place. For a call of this function, the list of arguments must specify, in last, an instance of univariate, the generic type 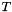$T$ is assumed to be a valid class of univariate polynomial. Example of such a call: 

   upoldse<...> p(...);
   univariate::reverse(p,i);

Definition at line 716 of file univariate.hpp.

References mmx::sparse::swap().

{ for ( int i = 0; i < n/2; i++ ) std::swap(p[i],p[n-i]) ; }
void scale ( R &  r,
const R &  p,
const C &  l 
)

Scale the variable in the polynomial p by l and put the result r. It computes the coefficients of the polynomial 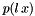$p(l \, x)$.

Definition at line 812 of file univariate.hpp.

Referenced by convertm2b(), and mmx::scale().

{
  r=p;
  C s(l);
  for(unsigned i=1; i< p.size();i++){
    r[i]*=s;
    s *=l;
  }
}
void mmx::univariate::set_monomial ( R &  x,
const C &  c,
unsigned  n 
) [inline]

Definition at line 418 of file univariate.hpp.

References checkdegree(), and mmx::array::set_cst().

  {

    x.resize(n+1);
    array::set_cst(x,(typename R::value_type)0);
    x[n]=c;
    checkdegree(x);

  }
void mmx::univariate::shift ( monomials< C > &  r,
const monomials< C > &  p,
int  d,
int  v = 0 
) [inline]

Definition at line 318 of file univariate.hpp.

References degree().

Referenced by convertm2b(), shift(), and mmx::shift().

                                                            {
    if(d>=0) {
      r.resize(degree(p)+d+1);
      for(int i=0; i<d;i++) 
        r[i]= (typename Polynomial::coeff_t)0;
      for(int i=0; i<=degree(p);i++) 
        r[i+d]=p[i];
    }
  }
void mmx::univariate::shift ( R &  r,
const R &  p,
const C &  x0 
)

Shift the polynomial p at the point x0 and put the result in r. In other words, it computes the coefficients of the polynomial 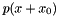$p(x+x_{0})$.

Definition at line 790 of file univariate.hpp.

References shift().

{
  r=p; shift(r,x0);
}
void mmx::univariate::shift ( R &  p,
const C &  c 
)

Inplace shift of the polynomial r at the point x0. It computes the coefficients of the polynomial 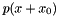$p(x+x_{0})$.

Definition at line 778 of file univariate.hpp.

{
  int j,k,s;
  for ( s = p.size(), j = 0; j <= s-2; j++ )
    for( k = s-2; k >= j; p[k] += c*p[k+1], k-- ) ;
};
int mmx::univariate::sign_at ( const POL &  p,
const X &  x 
) [inline]

Definition at line 547 of file univariate.hpp.

References eval_horner(), and mmx::sign().

  {
    X v= eval_horner(p,x);
    return sign(v);
  }
void mmx::univariate::sub ( monomials< C > &  r,
const monomials< C > &  a,
const monomials< C > &  b 
) [inline]

Definition at line 250 of file univariate.hpp.

References check_degree().

Referenced by div_rem(), use< operators_of, univariate::monomials< C > >::sub(), and sub().

                                                                {
    array::sub(r,a,b);
    check_degree(r);
  }
void mmx::univariate::sub ( monomials< C > &  r,
const monomials< C > &  a,
const C &  c 
) [inline]

Definition at line 262 of file univariate.hpp.

References check_degree(), degree(), and Polynomial.

                                                      {
    if(degree(a)>-1) {
      r=a; r[0]-=c;
    }
    else
      r= Polynomial(-c,0);
    check_degree(r);
  }
void mmx::univariate::sub ( monomials< C > &  r,
const monomials< C > &  a,
const X &  x 
) [inline]

Definition at line 272 of file univariate.hpp.

References sub().

                                                      {
    sub(r,a,(C)x);
  }
void mmx::univariate::sub ( monomials< C > &  r,
const C &  c 
) [inline]

Definition at line 277 of file univariate.hpp.

References check_degree(), degree(), and Polynomial.

                                 {
    if(degree(r)>-1) {
     r[0]-=c;
    }
    else
      r= Polynomial(-c,0);
    check_degree(r);
  }
void mmx::univariate::sub ( monomials< C > &  r,
const monomials< C > &  a 
) [inline]

Definition at line 256 of file univariate.hpp.

References check_degree(), and sub().

                                          {
    array::sub(r,a);
    check_degree(r);
  }
void mmx::univariate::sub_cst ( R &  r,
const S &  c 
) [inline]

Definition at line 432 of file univariate.hpp.

{ r[0]-=c;}
R::value_type mmx::univariate::tcoeff ( const R &  p) [inline]

Return the tail coefficient of the polynomial p.

Definition at line 363 of file univariate.hpp.

{ return p[0]; }