Public Member Functions

solver_series_rep (nat m, const vector< vector< C > > &init)
virtual void Increase_order (nat l)
virtual syntactic name_component (nat i)
virtual vector< series
< unknown< C, V > > > initialize ()=0
vector< series< unknown< C, V > > > me ()
vector< C > next ()

Public Attributes

nat m
vector< series< unknown< C, V > > > eqs
nat cur_n
vector< unknown< C, V > > sys

Detailed Description

template<typename C, typename V = typename Series_variant(C)>
class mmx::solver_series_rep< C, V >

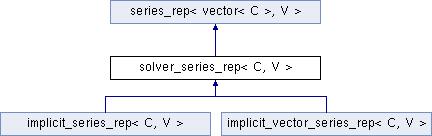
Definition at line 99 of file series_implicit.hpp.

Constructor & Destructor Documentation

solver_series_rep	(	nat	m,
		const vector< vector< C > > &	init
	)		`[inline]`

Definition at line 425 of file series_implicit.hpp.

References mmx::N().

                                                                    :
  VSeries_rep (format<VC > (/*FIXME*/)), m (m2), cur_n (0)
{
  this->n= N(init);
  Set_order (this->n);
  for (nat i=0; i<this->n; i++)
    this->a[i]= init[i];
}

Member Function Documentation

void Increase_order ( nat l ) [virtual]

Definition at line 435 of file series_implicit.hpp.

References mmx::increase_order(), and mmx::N().

                                 {
  VSeries_rep::Increase_order (l);
  for (nat i=0; i<N(eqs); i++)
    increase_order (eqs[i], l);
}

virtual vector< series< unknown<C,V> > > initialize ( ) [pure virtual]

Implemented in implicit_series_rep< C, V >, and implicit_vector_series_rep< C, V >.

vector< series< unknown< C, V > > > me ( )

Definition at line 448 of file series_implicit.hpp.

References mmx::unknown_series().

Referenced by implicit_vector_series_rep< C, V >::initialize(), and implicit_series_rep< C, V >::initialize().

                {
  vector<USeries > r= fill<USeries > (m);
  for (nat i=0; i<m; i++)
    r[i]= unknown_series (this, i);
  return r;
}

syntactic name_component ( nat i ) [virtual]

Definition at line 442 of file series_implicit.hpp.

References mmx::access(), and mmx::flatten().

                                 {
  if (m == 1) return syntactic ("f");
  else return access (syntactic ("f"), flatten (i+1));
}

vector< C > next ( )

Definition at line 456 of file series_implicit.hpp.

References mmx::C, mmx::insert_and_reduce(), mmx::is_exact_zero(), mmx::N(), Solver_rep, mmx::substitute(), UC, and VC.

                  {
  //mmerr << "Solving " << this->n << "\n";
  for (nat i=0; i<N(sys); i++)
    sys[i]= substitute (sys[i]);
  VC  ret = fill<C> (m);
  nat done= 0;
  while (true) {
    ASSERT (cur_n < this->n + 100, "too large delay in implicit solve");
    //mmerr << "  Coefficient " << cur_n << "\n";
    for (nat j=0; j<N(eqs); j++) {
      UC c= eqs[j][cur_n];
      //mmerr << "    Equation " << j << "= " << c << "\n";
      insert_and_reduce (sys, c);
    }
    //mmerr << "  System= " << sys << "\n";
    cur_n++;
    for (nat i=0; i<N(sys); i++)
      ASSERT (sys[i]->f == ((Solver_rep*) this) &&
              sys[i]->i1 >= this->n * m && sys[i]->i2 > this->n * m,
              "invalid situation during implicit solving");
    while (N(sys) > 0 && done < m) {
      UC c= sys[N(sys)-1];
      if (c->i2 <= this->n * m + done + 1) {
        nat j1 = c->i1 - this->n * m;
        nat j2 = min (done, c->i2 - this->n * m);
        C   rhs= c->b;
        for (nat j=j1; j<j2; j++)
          rhs += c->s[j-j1] * ret[j];
        if (c->i2 <= this->n * m + done) {
          ASSERT (is_exact_zero (rhs), "contradictory equations"); }
        else {
          ret[done]= -rhs / c->s[done-j1];
          //mmerr << "  Component " << done << "= " << ret[done] << "\n";
          done++;
        }
        sys.secure ();
        inside (sys) -> resize (N(sys) - 1);
      }
      else break;
    }
    if (done == m) return ret;
  }
}

Member Data Documentation

nat cur_n

Definition at line 103 of file series_implicit.hpp.

vector< series< unknown<C,V> > > eqs

Definition at line 102 of file series_implicit.hpp.

nat m

Definition at line 101 of file series_implicit.hpp.

vector< unknown<C,V> > sys

Definition at line 104 of file series_implicit.hpp.

The documentation for this class was generated from the following file:

/Users/mourrain/Devel/mmx/algebramix/include/algebramix/series_implicit.hpp