The general interface for matrix decomposition is given by the function: template<class Mthd, class Mat> Mat decomp(const Mat & m);
LU for Lower-Upper triangular decomposition.
QR for Orthogonal-Upper triangular decomposition.
Here are examples of its use: matrix_t T = Decomp<LU>(M);
matrix_t R = Decomp<QR>(M);
- See also:
synaps/linalg/decomp.h
Several methods for solving linear systems
![\[ A X = B \]](form_31.png)
where 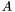 and
and 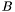 are
are 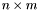 and
and 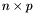 matrices. The result is a
matrices. The result is a 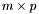 matrix. On can use the following methods
matrix. On can use the following methods
LU for solving using LU decomposition with column pivoting.
- LS for least square solving.
Here are examplesof its use. matrix_t B = ...;
matrix_t X = solve<LU>(A,B);
matrix_t Y = solve<LS>(A,B);
- See also:
synaps/linalg/solve.h
Different methods for computing the determinant of a matrix are discribed here: Gauss, Bareiss or Berkowitz methods.
LU for Gauss method uses classical pivoting techniques (ie. LU decomposition) to compute the determinant.
- Berkowitz method is based on the following recursion formula, based on Cayley-Hamilton identity:
![\[ d_0 : = \tmop{Trace} (A) ; A_0 : = A ; A_{k + 1} : = A_k A - \frac{1}{k + 1} \tmop{Trace} (A_k) A. \]](form_36.png)
- A mixed strategy, which expands the determinant with respect to the first row and Bareiss method is applied to the subdeterminants.
- See also:
synaps/linalg/Det.h
Definition: For a matrix 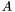 , the numerical rank of A is defined by: , the numerical rank of A is defined by:
![\[ \tmop{rank} (A, \epsilon) = \min \{\tmop{rank} (B) : \left| \frac{A}{\|A\|} - B \right| \leq \epsilon\}. \]](form_45.png)
|
The singular value decomposition of a matrix 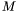 is the decomposition of the form
is the decomposition of the form
![\[ M = U \Sigma V^t \]](form_51.png)
where 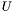 and
and 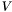 are orthognal matrices
are orthognal matrices 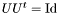 ,
, 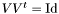 and
and 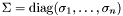 is a diagonal matrix such that
is a diagonal matrix such that 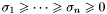 . The values
. The values 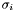 are called the singular values of
are called the singular values of 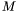 .
.
- See also:
synaps/linalg/svd.h
Theorem [*] shows that the smallest singular value is the distance between A and all the matrices of rank 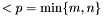 . Thus if
. Thus if 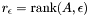 then
then
![\[ \sigma_1 \geq \cdots \geq \sigma_{r_{\epsilon}} > \epsilon \sigma_1 \geq \sigma_{r_{\epsilon + 1}} \geq \cdots \geq \sigma_p, \quad p = \min \{m, n\}. \]](form_60.png)
As a result, in order to determine the rank of a matrix  , we find the singular values
, we find the singular values 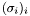 so that
so that
![\[ \tmop{rank} (A, \epsilon) = \max \{i ; \frac{\sigma_i}{\sigma_1} > \epsilon\}. \]](form_62.png)
The function
computes the rank of a matrix, as described above with a default value for 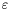 .
.
- See also:
synaps/linalg/rank.h
The computation of the eigenvalues and eigenvectors of a matrix are performed by the functions eigen and eigen_vect. They also provide generalised eigenvalues and eigenvectors, for pairs of matrices (a,B). If the internal representation of type lapack::rep2d<double>, the routine dgeeg or dgegv are called. - See also:
synaps/linalg/eigen.h
A set of functions are available, for performing FFT on generic vectors.
- See also:
synaps/linalg/FFT.h
![\[ a^{(k)}_{i, j} = \frac{a^{(k - 1)}_{i, j} a^{(k - 1)}_k - a^{(k - 1)}_{i, k} a^{(k - 1)}_{k, j}}{a^{(k - 2)}_{k - 1, k - 1}}, \]](form_24.png)
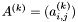 is the transformed matrix at step
is the transformed matrix at step 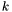 and
and 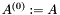 is the initial matrix. At the end of this process, after some permutation of the rows, the matrix is upper triangular. If A is a square matrix, the last entry
is the initial matrix. At the end of this process, after some permutation of the rows, the matrix is upper triangular. If A is a square matrix, the last entry 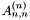 on the diagonal at the end of the process is the determinant of the matrix
on the diagonal at the end of the process is the determinant of the matrix 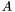 . Moreover, if
. Moreover, if 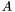 has its coefficients in a ring, it is the same for the matrices
has its coefficients in a ring, it is the same for the matrices 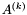 , since the previous division is exact
, since the previous division is exact![\[ A X = B \]](form_31.png)
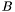 are
are 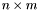 and
and 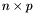 matrices. The result is a
matrices. The result is a 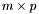 matrix. On can use the following methods
matrix. On can use the following methods![\[ d_0 : = \tmop{Trace} (A) ; A_0 : = A ; A_{k + 1} : = A_k A - \frac{1}{k + 1} \tmop{Trace} (A_k) A. \]](form_36.png)
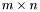 , there exists two orthogonal matrices
, there exists two orthogonal matrices ![\[ U = [u_1 \cdots, u_m] \in \mathbb{R}^{m \times m}, \tmop{and} V = [v_1, \cdots, \quad v_n] \in \mathbb{R}^{n \times n} \]](form_38.png)
![\[ U^t AV = \tmop{diag} (\sigma_1, \cdots, \sigma_p) \in \mathbb{R}^{m \times n} \quad p = \min \{m, n\} \tmtextrm{,} \]](form_39.png)
![\[ \sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_p \geq 0 \hspace{2em} \hspace{2em} \hspace{2em} \hspace{2em} \hspace{2em} \hspace{2em} \]](form_40.png)
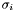 are called the
are called the 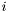 th singular value of A,
th singular value of A, 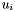 and
and 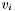 are respectively the
are respectively the ![\[ \tmop{rank} (A, \epsilon) = \min \{\tmop{rank} (B) : \left| \frac{A}{\|A\|} - B \right| \leq \epsilon\}. \]](form_45.png)
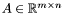 is of rank
is of rank 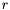 and
and 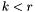 then
then ![\[ \sigma_{k + 1} = \min_{\tmop{rank} (B) = k} \|A - B\|. \]](form_49.png)
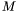 is the decomposition of the form
is the decomposition of the form ![\[ M = U \Sigma V^t \]](form_51.png)
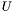 and
and 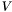 are orthognal matrices
are orthognal matrices 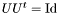 ,
, 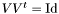 and
and 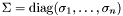 is a diagonal matrix such that
is a diagonal matrix such that 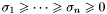 . The values
. The values 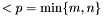 . Thus if
. Thus if 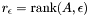 then
then ![\[ \sigma_1 \geq \cdots \geq \sigma_{r_{\epsilon}} > \epsilon \sigma_1 \geq \sigma_{r_{\epsilon + 1}} \geq \cdots \geq \sigma_p, \quad p = \min \{m, n\}. \]](form_60.png)
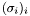 so that
so that ![\[ \tmop{rank} (A, \epsilon) = \max \{i ; \frac{\sigma_i}{\sigma_1} > \epsilon\}. \]](form_62.png)
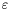 .
.