SYNAPS (SYmbolic Numeric ApplicationS) » Univariate Solvers

Real algebraic numbers

E. Tsigaridas

A real algebraic number is a real root of a polynomial, whose coefficients are integers. We represent such a real algebraic number, by a square-free polynomial and an isolating interval, that is an interval with rational endpoints, which contains only one root of the polynomial:

\begin{eqnarray*} \alpha \equiv \left( f (X), [a, b]) \right. & & \\ f \in \mathbbm{Z}[X] & & \\ a, b \in \mathbbm{Q} & & \end{eqnarray*}

The class for computing algebraic numbers

The class which specifies the construction of algebraic number is parameterised by a number type NT, corrresponding to the output type used to represent the algebraic numbers. It containts the following definitions: 
template < typename NT >
struct Algebraic 
{
  typedef NumberTraits<NT>   NTR;         // Number type traits 

  typedef typename NTR::RT   RT;          // Ring number type (typically 
  typedef typename NTR::FT   FT;          // Field number type (typically 
  typedef typename NTR::XT   XT;          // Approximate number type 
                                          // (typically double)
  typedef typename NTR::XIT RIT;          // Ring interval type
  typedef typename NTR::FIT FIT;          // Field interval type
  typedef typename NTR::XIT XIT;          // Approximate interval type

  typedef UPolDse<RT>       Poly;         // Univariate polynomial type
  typedef UPolDse<RT>       RT_Poly;      // Ring polynomial type
  typedef UPolDse<FT>       FT_Poly;      // Field polynomial type
  typedef UPolDse<XT>       XT_Poly;      // Approximate polynomial type
  typedef UPolDse<RL>       RL_Poly;      // Real polynomial type
  typedef ALGEBRAIC::root_of<RT, Poly> root_t;  // The root_of type
};
See also:
synaps/usolve/Algebraic.h.

Construction of algebraic numbers

The first way to define an algebraic number is to solve a polynomial, using the algebraic solver: 
   Seq< Algebraic<ZZ>::root_t > 
         solve(const UPolDse<ZZ> & P, Algebraic<ZZ> mth);
This returns a sequence of real algebraic numbers that are the roots of the polynomial P. If one is interested by a specific root, one can also use the following instructions: 
   Algebraic<ZZ>::root_t 
         solve(const UPolDse<ZZ> & P, Algebraic<ZZ> mth, int i);
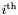which computes the $i^{\tmop{th}}$ root of P, if it exists. Otherwise, it produces an error. For polynomials of degree up to 4, we use precomputed discrimination systems in order to determine the square-free polynomial and we compute the isolating interval as function in the coefficients of the polynomial.

For polynomials of higher degree, we use a Sturm-like solver in order to isolate the roots of the polynomial.

Operations on real algebraic numbers

Currently, the available operations for the algebraic numbers are

o+

#include <synaps/upol.h>
#include <synaps/arithm/gmp.h>
#include <synaps/usolve/Algebraic.h>
typedef Algebraic<ZZ>::root_t root_t;

int main()
{
  using std::cout;
  using std::endl;

  UPolDse<ZZ> 
    p1("2*x^7+3*x^6+2*x^5+1*x^4-1*x^3-2*x^2-3*x+1"),
    p2("x^4-3*x^3+2*x^3-2*x^2-5*x+10"),
    p3("x^4-3*x^3+2*x^3-2*x^2-5*x+9");

  root_t 
    alpha= solve(p1,Algebraic<ZZ>(),1),
    beta = solve(p2,Algebraic<ZZ>(),0);

  cout<<"alpha: "<<alpha<<endl;
  //| root_of( 2*x^7+3*x^6+2*x^5+1*x^4-1*x^3-2*x^2-3*x+1, 1)
  //|  in [ 0,5/8 ], approx = 0.278212

  cout<<"beta : "<<beta <<endl;
  //| root_of( 1*x^4-1*x^3-2*x^2-5*x+10, 0 )
  //|  in [ 0,559/342 ], approx = 1.43343

  cout<<(alpha<beta)<<endl;
  //| 1

  cout <<sign_at(p1,beta)<<endl;
  //| 1

  cout <<sign_at(p2,beta)<<endl;
  //| 0

  cout <<sign_at(p3,beta)<<endl;
  //| -1
}

SYNAPS DOCUMENTATION
logo