It contains generic implementations on univariate (dense) polynomials. This set of functions apply when R provides the following methods or definitions:
|
Functions |
|
template<class OSTREAM, class POL> |
| OSTREAM & | lisp (OSTREAM &os, const POL &P) |
|
template<class C, class O, class R> |
| std::ostream & | print_as_coeff (std::ostream &os, const MPol< C, O, R > &p) |
|
template<class R> |
| int | degree (const R &p) |
| template<class R> |
| R::value_type | lcoeff (const R &p) |
| template<class R> |
| R::value_type | tcoeff (const R &p) |
|
template<class C> |
| std::ostream & | print_as_coeff (std::ostream &os, const C &c) |
|
template<class R> |
| std::ostream & | print (std::ostream &os, const R &p, char *x="x") |
|
template<class R, class C> |
| void | set_monomial (R &x, const C &c, unsigned n) |
|
template<class R, class S> |
| void | add_cst (R &r, const R &a, const S &c) |
|
template<class R, class S> |
| void | add_cst (R &r, const S &c) |
|
template<class R, class A, class B> |
| void | mul_index (R &r, const A &a, const B &b) |
|
template<class R> |
| void | mul_index_it (R &r, const R &a, const R &b) |
|
template<class R> |
| void | mul (R &r, const R &a, const R &b) |
|
template<class R> |
| void | mul (R &a, const R &b) |
|
template<class R> |
| void | mul_index (R &a, const R &b) |
|
template<class R> |
| void | mul_karatsuba (R &r, const R &a, const R &b) |
|
template<class C, class R> |
| C | eval_horner (const R &p, const C &c) |
|
template<class C, class R> |
| C | eval_horner_idx (const R &p, const C &c) |
|
template<typename POL, typename X> |
| int | sign_at (const POL &p, const X &x) |
|
template<class C, class R> |
| C | eval (const R &p, const C &c) |
|
template<class R> |
| void | div_rem (R &q, R &a, const R &b) |
|
template<class R> |
| void | checkdegree (R &p) |
| template<class R> |
| void | diff (R &r, const R &p) |
| template<class R> |
| R | diff (const R &p) |
| | Returns the derivative of the polynomial p.
|
| template<class R> |
| void | reciprocal (R &w, const R &p) |
|
template<class R> |
| void | reverse (R &p, typename R::size_type n) |
|
template<class R> |
| R::value_type | derive (const R p, typename R::value_type x) |
|
template<class R> |
| void | reduce (R &p, const typename R::size_type &e) |
| template<class R> |
| void | shift (R &t, const typename R::value_type &x0) |
| template<class R> |
| void | shift (R &t, const R &p, const typename R::value_type &x0) |
| template<class R, class C> |
| void | scale (R &t, const R &p, const C &l) |
| template<class T> |
| void | reduce (T &p, const typename T::size_type &e) |
| template<class T> |
| void | reverse (T &p, int n) |
| template<class O, class R, class I> |
| void | eval (O &p, O &dp, const R &Pol, const I &x) |
| template<class R> |
| R::value_type | derive (const R &Pol, const typename R::value_type &x) |
|
template<class R> |
| void | coeff_modulo (R &r, const typename R::value_type &x) |
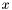 . Example:
. Example: 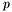 . The result is given in
. The result is given in 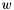 . We assume
. We assume ![$p[0] != 0$](form_6.png) . For this, we consider the equation
. For this, we consider the equation 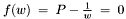 , where
, where 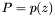 ,
, 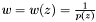 over the ring of formal power series in
over the ring of formal power series in 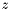 , and apply Newton's iteration to this equation. So we have :
, and apply Newton's iteration to this equation. So we have : 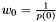 , and
, and 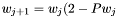 where
where 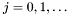 By reducing the different polynomials modulo
By reducing the different polynomials modulo 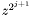 at each step, we have two convolutions of two pairs of vectors of dimensions at most
at each step, we have two convolutions of two pairs of vectors of dimensions at most 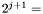 by step.
by step.
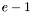 .
.
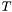 is assumed to be a valid class of univariate polynomial. Example of such a call:
is assumed to be a valid class of univariate polynomial. Example of such a call: 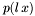 .
.
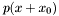 .
.
