
 Next: 20.3 Inflation
Up: 20 Opérateurs d'unicité
Previous: 20.1 Opérateur de Moore-Krawczyck
Next: 20.3 Inflation
Up: 20 Opérateurs d'unicité
Previous: 20.1 Opérateur de Moore-Krawczyck
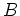 une boîte et
une boîte et 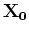 le milieu de
le milieu de 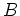
- la jacobienne du système a une inverse
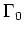 en
en 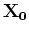 avec
avec
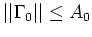
-
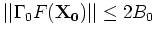
-
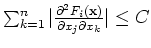 pour
pour
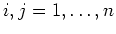 et
et 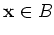
- les constantes
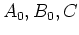 satisfont
satisfont
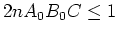
Alors
- il y a une solution unique pour
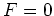 dans
dans
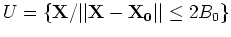
- la méthode de Newton initialisée avec
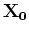 convergera
vers la solution
convergera
vers la solution
Utilisation: pour une boîte donnée
- calculer
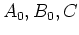 avec de l'arithmétique d'intervalles
avec de l'arithmétique d'intervalles
- calculer
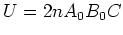 : si
: si
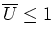 alors
alors
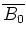 est le
diamètre d'une boîte centrée en
est le
diamètre d'une boîte centrée en 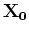 contenant une
solution unique de
contenant une
solution unique de 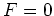 , calculable avec le schéma de Newton
, calculable avec le schéma de Newton
Exemple:
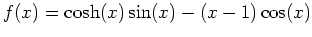
solution unique dans
![$[-3.4504,-3.41308]$](img195.png) ,
,
![$[-1.14694,-0.853064]$](img196.png) ,
,
![$[3.00813,3.42186]$](img197.png)

 Next: 20.3 Inflation
Up: 20 Opérateurs d'unicité
Previous: 20.1 Opérateur de Moore-Krawczyck
Jean-Pierre Merlet
Next: 20.3 Inflation
Up: 20 Opérateurs d'unicité
Previous: 20.1 Opérateur de Moore-Krawczyck
Jean-Pierre Merlet
2007-05-18