next up previous Next: Non-polynomial systems Up: benches Previous: benches

  • La page de J-P. Merlet
  • J-P. Merlet home page
  • La page Présentation de COPRIN
  • COPRIN home page
  • La page "Présentation" de l'INRIA
  • INRIA home page

    Subsections

    Polynomial systems

    Appolonius

    Origin: D. Cox, Ideals, Varieties and Algorithms, Springer-Verlag, 1992
    10 equations for 8 unknowns defined by: 

     
2*x1-2=0
 2*x2-1=0
 2*x3-2=0
 2*x4-1=0
 2*x5-x6=0
 x5+2*x6-2=0
 (x1-x7)^2+x8^2-x7^2-(x8-x2)^2=0
 (x1-x7)^2+x8^2-(x3-x7)^2-(x4-x8)^2=0
 x1^2+x2^2-2*x1*x7+2*x2*x8=0
 x1^2-x3^3-x4^2-2*x7*(x1-x3)+2*x4*x8=0
    Ranges: for all unknowns [-1e8,1e8]

    Solving method: GradientSolve+HullConsistencyStrong+ SimplexConsistency+3B
    Solutions:: 0
    Computation time (May 2004):

    DELL D400 (1.7Ghz) 0s

    Bellido

    Origin: [1]
    9 equations with 9 variables defined by: 

     
(z1-6)^2+z2^2+z3^2-104=0
 z4^2+(z5-6)^2+z6^2-104=0
 z7^2+(z8-12)^2+(z9-6)^2-80=0
z1*(z4-6)+z5*(z2-6)+z3*z6-52=0
 z1*(z7-6)+z8*(z2-12)+z9*(z3-6)+64=0
 z4*z7+z8*(z5-12)+z9*(z6-6)-6*z5+32=0
 2*z2+2*z3-2*z6-z4-z5-z7-z9+18=0
 z1+z2+2*z3+2*z4+2*z6-2*z7+z8-z9-38=0
 z1+z3+z5-z6+2*z7-2*z8-2*z4+8=0
    Ranges: for all unknowns [-1e8,1e8]

    Solving method: GradientSolve+HullConsistencyStrong+ SimplexConsistency+3B
    Solutions:: 8 (exact)
    Computation time (May 2004):

    Sun Blade 195s
    DELL D400 (1.7Ghz) 21s

    Bronstein

    Origin: COCONUT
    3 equations defined by: 

     
x^2 + y^2 + z^2 - 36=0
x+y - z=0
x*y + z^2 - 1=0
    Ranges: for all unknowns [-1e8,1e8]

    Solving method: GradientSolve+HullConsistencyStrong+3B
    Solutions:: 4 (exact)
    Computation time (May 2004)

    DELL D400 (1.7 GHz) 0.01s

    Brown

    Origin: [9]
    n equations defined by:

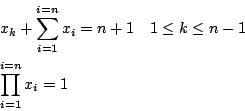
    \begin{eqnarray*} &&x_k+ \sum_{i =1}^{i = n}x_i =n+1   1\le k \le n-1 \\ &&\prod_{i =1}^{i = n}x_i = 1 \end{eqnarray*}

    solved here for n=5,30

    Ranges: for all unknowns [-1e8,1e8]

    Solving method: SolveSimplexGradient+HullConsistency+3B
    Solutions:: 3 for n=5, 2 for n=30 (exact)
    Computation time (April 2003):

    Sun Blade 1.23s (n=5), 9mn (n=30)

    Broyden banded

    Origin: [9]
    n equations defined by:

    \begin{displaymath} x_i(2+5 x_i ^2)+1-\sum_{j \in J_i} x_j(1+x_j) \end{displaymath}

    with ml=5, mu = 1 and

    \begin{displaymath} J_i = \{j, j \not= i, {\rm Max}(1,i-ml)\le j \le {\rm Min}(n,i+mu)\} \end{displaymath}

    solved here for n=10,30

    Ranges: for all unknowns [-100,100]

    Solving method: HessianSolve+HullConsistencyStrong+3B
    Solutions:: 1 for n=10, n=30 (exact)
    Computation time:

    Evo 410C (1.2GHz) 0.76s (n=10), 11mn (n=30) (April 2003)
    DELL D400 (1.7Ghz) 0.76s (n=10), 130s (n=30) (May 2004)

    Broyden tridiagonal

    Origin: [9]
    n equations defined by:

    \begin{displaymath} (3-2x_i)x_i-x_{i-1}-2x_{i+1}+1 \end{displaymath}

    with $x_0=x_{n+1}=0$,solved here for n=10,30

    Ranges: for all unknowns [-100,100]

    Solving method: GradientSolve+HullConsistencyStrong+ 3B
    Solutions:: 2 for n=10, 2 for n=30 (exact)
    Computation time:

    Evo 410C (1.2GHz) 0.55s (n=10), 112.98s (n=30) (April 2003)
    DELL D400 (1.7GHz) 0.24s (n=10), 26.14s (n=30) (May 2004)

    Caprasse

    Origin: FRISCO
    4 equations

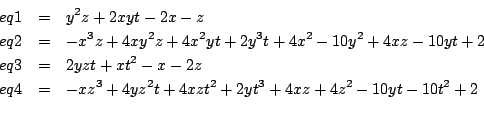
    \begin{eqnarray*} eq1&=&y^2 z+2 x y t-2 x-z\\ eq2&=&-x^3 z+4 x y^2 z+4 x^2 y t+... ...x z^3+4 y z^2 t+4 x z t^2+2 y t^3+4 x z+4 z^2-10 y t-10 t^2+2\\ \end{eqnarray*}

    y^2 z+2 x y t-2 x-z=0
-x^3 z+4 x y^2 z+4 x^2 y t+2 y^3 t+4 x^2-10 y^2+4 x z-10 y t+2=0
&2 y z t+x t^2-x-2 z=0
-x z^3+4 y z^2 t+4 x z t^2+2 y t^3+4 x z+4 z^2-10 y t-10 t^2+2=0
    Ranges: for all unknowns [-10,10]
    Solving method: HessianSolve+HullConsistency+3B
    Solutions:: 18 (exact)
    Computation time (April 2003):
    Sun Blade 30.15s
    EVO 410C (1.2Ghz) 6.71s

    Celestial

    Origin: FRISCO
    3 equations

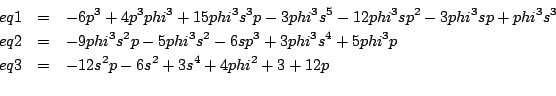
    \begin{eqnarray*} eq1&=&-6 p^3+4 p^3 phi^3+15 phi^3 s^3 p-3 phi^3 s^5-12 phi^3 s... ...3 s^4+5 phi^3 p\\ eq3&=&-12 s^2 p-6 s^2+3 s^4+4 phi^2+3+12 p\\ \end{eqnarray*}

    -6 p^3+4 p^3 phi^3+15 phi^3 s^3 p-3 phi^3 s^5-12 phi^3 s p^2
-3 phi^3 s p+phi^3 s^3=0
-9 phi^3 s^2 p-5 phi^3 s^2-6 s p^3+3 phi^3 s^4+5 phi^3 p=0
-12 s^2 p-6 s^2+3 s^4+4 phi^2+3+12 p=0
    Unknown Range
    p [0.001,1000]
    s [0.001,1000]
    phi [0.001,1000]
    Solving method: GradientSolve+HullConsistency+3B
    Solutions:: 2 (exact)
    Computation time (April 2003):
    Sun Blade 9.69s (April 2003)
    EVO 410C (1.2Ghz) 2.43s (April 2003)
    DELL D400 (1.7Ghz) 0.75s (May 2004)

    Chem

    Origin: COCONUT
    5 equations defined by: 

     
3*y5 - y1*(y2 + 1)=0
y2*(2*y1 + y3^2 + r8 + 2*r10*y2 + r7*y3 + r9*y4) +y1 - r*y5=0
y3*(2*y2*y3 + 2*r5*y3 + r6 + r7*y2) - 8*y5=0
y4*(r9*y2 + 2*y4) - 4*r*y5=0
y2*(y1+r10*y2+y3^2+r8+r7*y3+r9*y4)+y1+r5*y3^2+y4^2-1+r6*y3=0
    with 
     
 r = 10
 r5 = 0.193
 r6 = 0.002597/sqrt(40.)
 r7 = 0.003448/sqrt(40.)
 r8 = 0.00001799/40.
 r9 = 0.0002155/sqrt(40.)
 r10= 0.00003846/40.
    Ranges: for all unknowns [0,1e8] or [-1e8,1e8]

    Solving method: GradientSolve+HullConsistencyStrong+3B
    Solutions:: 1 for range [0,1e8], 4 for range [-1e8,1e8] (exact)
    Computation time (May 2004):

    DELL D400 (1.7 GHz) 0.05s (range =[0,1e8]), 0.5s (range =[-1e8,1e8])

    Chemk

    Origin: Kearfott, COCONUT
    4 equations defined by: 

     
x1^2 - x2 =0
x4^2 - x3 =0
2.177e7*x2 - 1.697e7*x2*x4 + 0.55*x1*x4 + 0.45*x1 - x4=0

1.585e14*x2*x4 + 4.126e7*x1*x3 - 8.282e6*x1*x4 + 
2.284e7*x3*x4 - 1.918e7*x3 + 48.4*x4 - 27.73=0
    Ranges: for all unknowns [0,1]

    Solving method: GradientSolve+HullConsistencyStrong+3B
    Solutions:: 1 (exact)
    Computation time (May 2004): will almost not change if the search space is extended to [-1e8,1e8]:

    DELL D400 (1.7 GHz) 0.01s

    Countercurrent reactors

    Origin: [8]
    n equations, a = 1/2

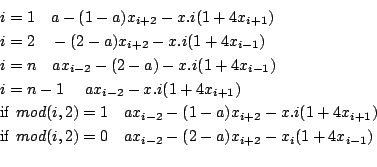
    \begin{eqnarray*} &&i =1   a-(1-a) x_{i+2}-x.i (1+4 x_{i+1})\\ &&i =2   -(2-a... ...rm if} mod(i,2)=0   a x_{i-2}-(2-a) x_{i+2}-x_i (1+4 x_{i-1})\\ \end{eqnarray*}

    Ranges: [-1e8,1e8] for all unknowns

    Solving method: HessianSolve+HullConsistency+ 3B
    Solutions:: 18 (n=10), 38 (n=20) (exact)
    Computation time:

    Evo 410C (1.2GHz) 6.52s (n=10) 1039.75s (n=20)(April 2003)
    DELL D400 (1.7Ghz) (1.2GHz) 3.22s (n=10) 570s (n=20)(May 2004)

    Cyclo

    Origin: FRISCO
    3 equations defined by: 

    -y^2*z^2-y^2+24*y*z-z^2-13=0
-x^2*z^2-x^2+24*x*z-z^2-13=0
 -x^2*y^2-x^2+24*x*y-y^2-13=0
    Ranges: for all unknowns [0,100000]
    Solving method: HessianSolve+HullConsistency+ SimplexConsistency
    Solutions:: 8 (exact)
    Computation time (April 2003):
    Sun Blade 2.11s
    EVO 410C (1.2Ghz) 0.38s

    Dietmaier

    Origin: Dietmaier  [4]
    Physical meaning: forward kinematics of a parallel robot. Six points in a known position are chosen on two rigid bodies M1, M2. The set of points on M1 is A1,A2,..A6 and B1,B2,..B6 on M2. The distance between the 6 pairs (Ai,Bi) is known and the purpose of the system is to determine the possible location of M2 with respect to M2 (it can be shown that there will be at most 40 solutions)
    12 equations:

    \begin{eqnarray*} &&xb_1^2+yb_1^2+zb_1^2- 1.0=0\\ &&(xb_2- 1.107915)^2+yb_2^2+z... ....2758935157 zb_3+ 0.2523375480 zb_4+ 0.205018)^2- 0.5945504870=0 \end{eqnarray*}

    xb_1^2+yb_1^2+zb_1^2- 1.0=0
(xb_2- 1.107915)^2+yb_2^2+zb_2^2- 0.4163798256=0
(xb_3- 0.549094)^2+(yb_3-0.756063)^2+zb_3^2- 1.180012929=0
(xb_4- 0.735077)^2+(yb_4+0.223935)^2+(zb_4- 0.525991)^2- 2.260328827=0
(xb_1-xb_2)^2+(yb_1-yb_2)^2+(zb_1-zb_2)^2- 0.2946372680=0
(xb_1-xb_3)^2+(yb_1-yb_3)^2+(zb_1-zb_3)^2- 1.195445050=0
(xb_1-xb_4)^2+(yb_1-yb_4)^2+(zb_1-zb_4)^2- 2.535465199=0
(xb_2-xb_3)^2+(yb_2-yb_3)^2+(zb_2-zb_3)^2- 0.4512414822=0
(xb_2-xb_4)^2+(yb_2-yb_4)^2+(zb_2-zb_4)^2- 2.107211052=0
(xb_3-xb_4)^2+(yb_3-yb_4)^2+(zb_3-zb_4)^2- 2.082590368=0
(- 1.574393890 xb_1+ 4.739721238 xb_2- 2.242096748 xb_3+ 0.07676939964 xb_4- 0.514188)^2+(- 1.574393890 yb_1+ 4.739721238 yb_2- 2.242096748 yb_3+0.07676939964 yb_4+ 0.526063)^2+(- 1.574393890 zb_1+ 4.739721238 zb_2- 2.242096748 zb_3+ 0.07676939964 zb_4+ 0.368418)^2- 1.643352216=0
( 1.520253264 xb_1- 1.048484327 xb_2+ 0.2758935157 xb_3+ 0.2523375480 xb_4- 0.590473)^{2}+( 1.520253264 yb_1- 1.048484327 yb_2+ 0.2758935157 yb_3+ 0.2523375480 yb_4- 0.094733)^2+( 1.520253264 zb_1- 1.048484327 zb_2+ 0.2758935157 zb_3+0.2523375480 zb_4+ 0.205018)^2- 0.5945504870=0
    Unknowns:
    $xb_1,yb_1,zb_1,xb_2,yb_2,zb_2,xb_3 ,yb_3,zb_3,xb_4,yb_4,zb_4$

    Ranges: may be chosen arbitrary large without any change in the computation time

    Solving method: SolveDistance
    Solutions:: 40 (exact)
    Computation time (April 2003):

    EVO 410C (1.2Ghz) 22s

    Dipole2

    Origin: COCONUT, modified by COPRIN (original problem: see Dipole)
    4 equations defined by: 

     
a+b=0.63254
 c+d =-1.34534
 t*a+u*b-v*c-w*d=-0.8365348
 v*a+w*b+t*c+u*d=1.7345334
 a*t**2-a*v**2-2*c*t*v+b*u**2-b*w**2-2*d*u*w=1.352352
 c*t**2-c*v**2+2*a*t*v+d*u**2-d*w**2+2*b*u*w=-0.843453
a*t**3-3*a*t*v**2+c*v**3-3*c*v*t**2+b*u**3-3*b*u*w**2+d*w**3-3*d*w*u**2= 
-0.9563453
c*t**3-3*c*t*v**2-a*v**3+3*a*v*t**2+ d*u**3-3*d*u*w**2-b*w**3+3*b*w*u**2=1.2342523
    The 4 first equations are linear in $a,b,c,d$. They are solved to get a system in $u,v,t,w$ Ranges: for all unknowns [-1000,1000]
    Solving method: HessianSolve+HullConsistency+3B+SimplexConsistency
    Solutions:: 2 (exact)
    Computation time (April 2007):
    Dell D620 (1.7Ghz) 69.72s

    Discrete boundary value function

    Origin: [9]
    n equations defined with h=1/(n+1), ti = ih

    \begin{displaymath} 2x_i-x_{i-1}-x_{i+1}+h^2(x_i+ti+1)^3/2 \end{displaymath}

    with $x_0=x_{n+1}=0$,solved here for n=20, 40

    Ranges: for all unknowns [-100,100]

    Solving method: HessianSolve+HullConsistency+3B
    Solutions:: 1 for n=20, 1 for n=40 (exact)
    Computation time (April 2003):

    Evo 410C (1.2Ghz) 1.13s (n=20), 22.92s (n=40)

    Discrete integral

    Origin: [9]
    n equations defined with h=1/(n+1), ti = ih

    \begin{displaymath} x_i+h [\sum_{j=1}^{j=i}t_j(x_j+t_j+1)^3+\sum_{j=i+1}^{j=n}(1-t_j)(x_j+t_j+1)^3] \end{displaymath}

    with $x_0=x_{n+1}=0$

    Ranges: for all unknowns [-100,100]
    Solving method: HessianSolve+HullConsistency+3B (until May 2004), GlobalConsistencyTaylor, IntervalNewton and special 2B (2007)
    Solutions:: 3 for n=5, 8,9,20, 1 for n=1,7,10,11 (exact)
    Computation time:

    Evo 410C (1.2GHz) 40.46s (n=5), 915.97s (n=6) (April 2003)
    DELL D400 (1.7 GHz) 5.63s (n=5), 105.47s (n=6) (May 2004)
    Cluster (11 PC's) 3776s (n=7) (April 2003)
    DELL D620 (1.7Ghz) 0.027s (n=5), 0.032s(n=6), 0.045s(n=7), 1.15s (n=8), 1.39s (n=9), 2.58s (n=10), 2.98s (n=11), 1mn42s (n=20)

    Note that until 2007 this system was considered as a difficult one

    This system may be changed into another system of 2n equations in the unknowns y1..yn,x1..xn defined by:

    \begin{eqnarray*} &&x_j=(y_j+t_j+1)^3\\ &&y_j+h [\sum_{j=1}^{j=i}t_jx_j+\sum_{j=i+1}^{j=n}(1-t_j)x_j]\\ \end{eqnarray*}

    Ranges: for all yj [-100,100], for all xj [-1000000,1000000]
    Solving method: HessianSolve+HullConsistency+ SimplexConsistency+3B
    Solutions:: 1 for n=6, 1 for n=20 (exact)
    Computation time (April 2003):

    Evo 410C (1.2Ghz) 7.7s (n=6), 375.8s (n=20)

    Eco9

    Origin: COCONUT [13]
    8 equations with 8 unknowns: 

     
x1 + x2*(x1 + x3) + x4*(x3 + x5) + x6*(x5 + x7) -( x8*((1/8) - x7))=0
x2 + x3*(x1 + x5) + x4*(x2 + x6) + x5*x7 -( x8*((2/8) - x6))=0
x3*(1 + x6) + x4*(x1 + x7) + x2*x5 -( x8*((3/8) - x5))=0
x4 + x1*x5 + x2*x6 + x3*x7 -( x8*((4/8) - x4))=0
x5 + x1*x6 + x2*x7 -( x8*((5/8) - x3))=0
x6 + x1*x7 -( x8*((6/8) - x2))=0
x7 -( x8*((7/8) - x1))=0
x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 +1=0
    Ranges: [-100,100] for all unknowns

    Solving method: GradientSolve+HullConsistencyStrong+ +3B
    Solutions:: 16 (exact)
    Computation time (May 2004):

    DELL D400 (1.7 Ghz) 208s

    Equilibrium Combustion

    Origin: [6]
    6 equations

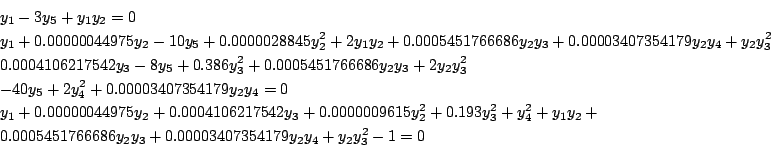
    \begin{eqnarray*} &&y_1-3 y_5+y_1 y_2 =0\\ &&y_1+ 0.00000044975 y_2-10 y_5+ 0.... ...0005451766686 y_2 y_3+ 0.00003407354179 y_2 y_4+y_2 y_3^2-1=0\\ \end{eqnarray*}

     
y_1-3 y_5+y_1 y_2
y_1+0.00000044975 y_2-10 y_5+0.0000028845 y_2^2+2 y_1y_2+
0.0005451766686 y_2 y_3+0.00003407354179 y_2 y_4+y_2y_3^2

0.0004106217542 y_3-8 y_5+0.386 y_3^2+0.0005451766686 y_2y_3+2 y_2y_3^2
-40 y_5+2 y_4^2+0.00003407354179 y_2y_4

y_1+0.00000044975 y_2+0.0004106217542 y_3+0.0000009615y_2^2+
0.193 y_3^2+y_4^2+y_1y_2+0.0005451766686 y_2 y_3+0.00003407354179 y_2y_4+y_2y_3^2-1
    Ranges: [-1e8,1e8] for all unknowns

    Solving method: HessianSolve+HullConsistency+ SimplexConsistency+3B
    Solutions:: 4 (exact)
    Computation time (April 2003):

    Evo 410C (1.2Ghz) 2s

    Extended Freudenstein

    Origin: [8]
    Physical meaning: none
    n equations:

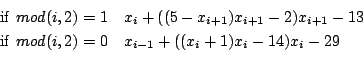
    \begin{eqnarray*} &&{\rm if}  mod(i,2)=1   x_i+((5-x_{i+1})x_{i+1}-2)x_{i+1}-13\\ &&{\rm if} mod(i,2)=0   x_{i-1}+((x_i+1)x_i-14)x_i-29\\ \end{eqnarray*}

    Ranges: [-1e8,1e8] for all unknowns
    Solving method: HessianSolve+HullConsistency+3B
    Solutions:: 1 (exact)
    Computation time (April 2003):

    EVO 410C (1.2Ghz) 5.2s (n=20)

    Extended Powell1

    Origin: [8]
    n=4m equations:

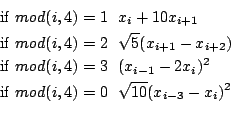
    \begin{eqnarray*} &&{\rm if} mod(i,4)=1  x_i+10x_{i+1}\\ &&{\rm if} mod(i,4)=2 ... ...1}-2x_i)^2\\ &&{\rm if} mod(i,4)=0  \sqrt{10}(x_{i-3}-x_i)^2\\ \end{eqnarray*}

    Ranges: [-1e8,1e8]

    Solving method: HessianSolve+HullConsistency+3B
    Solutions:: 4 (n=16) (approximate)
    Computation time (April 2003):

    Evo 410C (1.2Ghz) 3.33s (n=16)

    Extended Wood

    Origin: [8]
    n=4m equations:

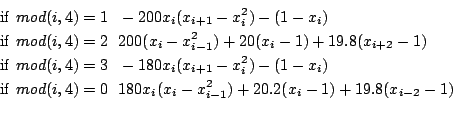
    \begin{eqnarray*} &&{\rm if} mod(i,4)=1  -200x_i(x_{i+1}-x^2_i)-(1-x_i)\\ &&{\r... ...mod(i,4)=0  180x_i(x_i-x^2_{i-1})+20.2(x_i-1)+19.8(x_{i-2}-1)\\ \end{eqnarray*}

    Ranges: [-1e8,1e8]

    Solving method: HessianSolve+HullConsistency+ 3B + IntervalNewton (since May 2007)
    Solutions:: 3 (n=4), 9 (n=8), 27 (n=12), 81 (n=16) (exact)
    Computation time

    Evo 410C (April 2003): (1.2Ghz) 4.41s (n=4), 269.29s (n=8)
    DELL 620 (May 2007) (1.7GHz) 21.16s (n=8), 3mn5s (n=12), 38mn8s (n=16)
    Note that this problem was intially classified as a difficult problem.

    Fourbar

    Origin: COCONUT
    4 equations defined by: 
     
0.01692601*X1^2*Y1^2 - 0.888509280014*X1^2*Y2^2
+ 0.0411717692438*X2^2*Y1^2 - 0.00437457395884*X2^2*Y2^2
+ 0.331480641249*X1*X2*Y1^2 - 1.38036964668*X1*X2*Y2^2
- 0.270492270191*X1^2*Y1*Y2 + 1.44135801774*X2^2*Y1*Y2
+ 0.859888946812*X1*X2*Y1*Y2
+ 0.0791489659197*X1^2*Y1 - 0.00336032777032*X1^2*Y2
- 0.0620826738427*X1*Y1^2 + 0.501879647495*X1*Y2^2
+ 0.647156236961*X2^2*Y1 + 0.0926311741907*X2^2*Y2
- 0.255000006226*X2*Y1^2 - 0.0896892386081*X2*Y2^2
- 0.568007271041*X1*X2*Y2 + 0.095991501961*X1*X2*Y1
+ 0.165310767618*X1*Y1*Y2 - 0.563962321337*X2*Y1*Y2
- 0.0784871167595*X1*Y1 - 0.0784871167595*X2*Y2
+ 0.011807283256*X1*Y2  - 0.011807283256*X2*Y1
+ 0.0422876985355*X1^2 + 0.0422876985355*X2^2
+ 0.0372427422943*Y1^2 + 0.0372427422943*Y2^2=0

0.518178672335*X1^2*Y1^2 - 0.0414464807343*X1^2*Y2^2
+ 2.63600135179*X2^2*Y1^2 - 0.799490472298*X2^2*Y2^2
+ 0.29442805494*X1^2*Y1*Y2 + 1.46551534655*X2^2*Y1*Y2
- 0.631878110759*X1*X2*Y1^2 - 1.80296540237*X1*X2*Y2^2
- 2.87586667102*X1*X2*Y1*Y2
- 0.987856648177*X1^2*Y1 - 0.530579106676*X1^2*Y2
- 0.0397576281649*X1*Y1^2 + 0.317719102869*X1*Y2^2
- 1.93710490787*X2^2*Y1  + 0.00127693327315*X2^2*Y2
- 0.581380074072*X2*Y1^2 - 0.0672137066743*X2*Y2^2
+ 0.531856039949*X1*X2*Y1 + 0.949248259696*X1*X2*Y2
+ 0.514166367398*X1*Y1*Y2 - 0.357476731033*X2*Y1*Y2
+ 0.140965913657*X1*Y1  + 0.140965913657*X2*Y2
- 0.153347218606*X1*Y2  + 0.153347218606*X2*Y1
+ 0.283274882058*X1^2  + 0.283274882058*X2^2
+ 0.0382903330079*Y1^2 + 0.0382903330079*Y2^2 =0

0.0233560008057*X1^2*Y1^2 - 0.00428427501149*X1^2*Y1*Y2
- 0.792756311827*X1^2*Y2^2 + 0.0492185850289*X2^2*Y2^2
+ 0.0759264856293*X1*X2*Y1^2 + 1.14839711492*X1*X2*Y1*Y2
- 0.283066217262*X2^2*Y1^2 + 0.460041521291*X2^2*Y1*Y2
 - 0.388399310674*X1*X2*Y2^2
- 0.0561169736293*X1*Y1^2 + 0.485064247792*X1*Y2^2
+ 0.0689567235492*X1^2*Y1 - 0.115620658768*X1^2*Y2
- 0.13286905328*X2*Y1^2 - 0.084375901147*X2*Y2^2
+ 0.639964831612*X2^2*Y1 + 0.101386684276*X2^2*Y2
+ 0.217007343044*X1*X2*Y1 - 0.571008108063*X1*X2*Y2
+ 0.0484931521334*X1*Y1*Y2 - 0.541181221422*X2*Y1*Y2
- 0.00363197918253*X1*Y2 + 0.00363197918253*X2*Y1
- 0.0781302968652*X1*Y1 - 0.0781302968652*X2*Y2
+ 0.0471311092612*X1^2 + 0.0471311092612*X2^2
+ 0.0324495575052*Y1^2 + 0.0324495575052*Y2^2 ;

0.393707415641*X1^2*Y1^2 + 0.59841456862*X1^2*Y2^2
+ 0.0735854940135*X2^2*Y1^2 + 0.0548997238169*X2^2*Y2^2
+ 0.0116156836985*X1^2*Y1*Y2 + 0.0699694273575*X2^2*Y1*Y2
- 0.305757340849*X1*X2*Y1^2 - 0.364111084508*X1*X2*Y2^2
- 0.223392923175*X1*X2*Y1*Y2
+ 0.0996725944534*X1^2*Y1 + 0.0113936468426*X1^2*Y2
- 0.381205205249*X1*Y1^2 - 0.473402150235*X1*Y2^2
- 0.0213613191759*X2^2*Y1 - 0.0372595571271*X2^2*Y2
+ 0.148904552394*X2*Y1^2 + 0.142408744984*X2*Y2^2
- 0.0486532039697*X1*X2*Y1 + 0.121033913629*X1*X2*Y2
- 0.00649580741066*X1*Y1*Y2 + 0.092196944986*X2*Y1*Y2
- 0.0483106652705*X1*Y1  - 0.0483106652705*X2*Y2
- 0.00316794272326*X1*Y2 + 0.00316794272326*X2*Y1
+ 0.00634952598374*X1^2 + 0.00634952598374*X2^2
+ 0.0922886309144*Y1^2  + 0.0922886309144*Y2^2 =0
    Ranges: for all unknowns [-10,10]

    Solving method: GradientSolve+HullConsistency+ +3B
    Solutions:: 3 (2 exact, 1 singular)
    Computation time (September 2004):

    DELL D400 (1.7Ghz) 364s

    Geneig

    Origin: COCONUT
    Physical meaning: generalized eigenvalue problem

    6 equations: 

     
-10*x1*x6^2+ 2*x2*x6^2-x3*x6^2+x4*x6^2+ 3*x5*x6^2+x1*x6+ 2*x2*x6+x3*x6+ 2*x4*
x6+x5*x6+ 10*x1+ 2*x2-x3+ 2*x4-2*x5 =0

2*x1*x6^2-11*x2*x6^2+ 2*x3*x6^2-2*x4*x6^2+x5*x6^2+ 2*x1*x6+x2*x6+ 2*x3*x6+x4*
x6+ 3*x5*x6+ 2*x1+ 9*x2+ 3*x3-x4-2*x5 =0

-x1*x6^2+ 2*x2*x6^2-12*x3*x6^2-x4*x6^2+x5*x6^2+x1*x6+ 2*x2*x6-2*x4*x6-2*x5*x6-
x1+ 3*x2+ 10*x3+ 2*x4-x5 =0

x1*x6^2-2*x2*x6^2-x3*x6^2-10*x4*x6^2+ 2*x5*x6^2+ 2*x1*x6+x2*x6-2*x3*x6+ 2*x4*
x6+ 3*x5*x6+ 2*x1-x2+ 2*x3+ 12*x4+x5 =0

3*x1*x6^2+x2*x6^2+x3*x6^2+ 2*x4*x6^2-11*x5*x6^2+x1*x6+ 3*x2*x6-2*x3*x6+ 3*x4*
x6+ 3*x5*x6-2*x1-2*x2-x3+x4+ 10*x5 =0

x1+x2+x3+x4+x5-1 :
    Ranges: [-1e8,1e8] for all unknowns
    Solving method: GradientSolve+HullConsistencyStrong+3B
    Solutions:: 10 (exact)
    Computation time (May 2004):
    DELL D400 (1.7Ghz) 108s

    Eiger-Sikorski-Stenger

    Origin: [7]
    n equations:

    \begin{eqnarray*} &&(x_i-0.01)^2+x_{i+1}   i\in [1,n-1]\\ &&(x_n-0.1)+x_1-0.1 \end{eqnarray*}

    Ranges: [-1e8,1e8]

    Solving method: HessianSolve+HullConsistency+ 3B
    Solutions:: 2 (exact)
    Computation time

    DELL 620 (May 2007) (1.7GHz) 0.012s (n=9), 1.49s (n=20), 9.96s (n=30)

    Freudenstein

    Origin: [9]
    Physical meaning: none
    2 equations

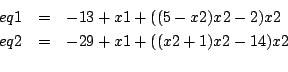
    \begin{eqnarray*} eq1&=&-13+x1+((5-x2)x2-2)x2\\ eq2&=&-29+x1+((x2+1)x2-14)x2\\ \end{eqnarray*}

    -13+x1+((5-x2)*x2-2)*x2
-29+x1+((x2+1)*x2-14)*x2
    Ranges: [-1e8,1e8] for x1, x2
    Solving method: HessianSolve+HullConsistency+3B
    Note that we don't use the difference between the two equations
    Solutions:: 1 (exact)
    Computation time (April 2003):
    EVO 410C (1.2Ghz) 0.04s

    Himmelblau

    Origin: [9]
    2 equations

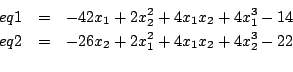
    \begin{eqnarray*} eq1&=&-42 x_1 + 2 x_2^2 + 4 x_1 x_2 + 4 x_1^3 - 14\\ eq2&=&-26 x_2 + 2 x_1^2 + 4 x_1 x_2 + 4 x_2^3 - 22\\ \end{eqnarray*}

    Ranges: [-1e8,1e8] for x1, x2

    Solving method: HessianSolve+HullConsistency+3B

    Solutions:: 9 (exact)
    Computation time (April 2003):

    EVO 410C (1.2Ghz) 0.11s

    I5

    Origin: COCONUT [13]
    10 equations with 10 unknowns: 

     
 x1  - 0.18324757*(x4*x3*x9)^3  + x3^4*x9^7  - 0.25428722=0
 x2  - 0.16275449*(x1*x10*x6)^3 + x10^4*x6^7 - 0.37842197=0
 x3  - 0.16955071*(x1*x2*x10)^3 + x2^4*x10^7 - 0.27162577=0
 x4  - 0.15585316*(x7*x1*x6)^3  + x1^4*x6^7  - 0.19807914=0
 x5  - 0.19950920*(x7*x6*x3)^3  + x6^4*x3^7  - 0.44166728=0
 x6  - 0.18922793*(x8*x5*x10)^3 + x5^4*x10^7 - 0.14654113=0
 x7  - 0.21180486*(x2*x5*x8)^3  + x5^4*x8^7  - 0.42937161=0
 x8  - 0.17081208*(x1*x7*x6)^3  + x7^4*x6^7  - 0.07056438=0
 x9  - 0.19612740*(x10*x6*x8)^3 + x6^4*x8^7  - 0.34504906=0
x10 - 0.21466544*(x4*x8*x1)^3  + x8^4*x1^7  - 0.42651102=0
    Ranges: [-1,1] or [-100,100] for all unknowns

    Solving method: GradientSolve+HullConsistencyStrong+ +3B
    Solutions:: 1 for range [-1,1], 30 for range [-100,100] (exact)
    Computation time (May 2004):

    DELL D400 (1.7GHz) 0.02s (range [-1,1]), 397s (range [-100,100])

    Kapur

    Origin: COCONUT
    9 equations defined by: 

     
 y*u1 + u3 - a=0
 x*u1 + u3 - b=0
 w*u2 + u4 - c=0
 z*u2 + u4 - d=0
 2*u4*u1 + 2*u3*u2 - 9*t=0
 u1 - (z+w)=0
 u2 - (x+y)=0
 u3 - w*z=0
 u4 - x*y=0
    This is a modified version of the original system 
     
y*z + z*w + w*y - a=0
z*x + x*w + w*z - b=0
w*x + x*y + y*w - c=0
x*y + y*z + z*x - d=0
2*x*y*z + 2*y*z*w + 2*z*w*x + 2*w*x*y - 9*t=0

    Ranges: [-1e8,1e8] for u1,u2,u3,u4, [0,1000] for x,y,z,w,t

    Solving method: GradientSolve+HullConsistencyStrong+3B
    Solutions:: 1 (exact)
    Computation time (May 2004)

    DELL D400 (1.7 GHz) 0.02s (original) 0.03s (modified)

    Katsura n

    Origin: Faugère, http://www-calfor.lip6.fr
    Physical meaning: the unknowns is the value of a distribution function of a field created by a mixture of a ferro antiferro magnetic bond at some some points. Hence the unknowns are probabilities and should lie in [0,1]

    To respect the classical denomination in the bench of algebraic systems Katsura n has n+1 equations.

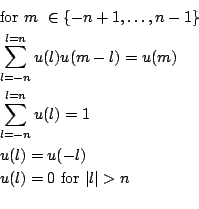
    \begin{eqnarray*} &&{\rm for} m  \in \{-n+1,\ldots,n-1\} \\ && \sum_{l=-n}^{l=n... ...n}u(l)=1\\ &&u(l)=u(-l)\\ &&u(l)=0 {\rm for} \vert l\vert>n\\ \end{eqnarray*}

    Unknowns: u(0),u(1),...u(n)
    Ranges: [0,1]
    Solving method: HessianSolve+HullConsistency+ SimplexConsistency+3B
    Solutions:: 4 (n=9), 7 (n=12), 3 (n=13), 5 (n=14), 5 (n=15), 7 (n=20) (exact)
    Computation time (April 2003):

    EVO 410C (1.2GHz) 21.61s (n=9), 514.86s (n=12), 1077s (n=13), 2948s (n=14)
    Cluster (12 PC's) 37mn (n=15), 6h55mn (n=20)

    Kearl11

    Origin: COCONUT
    8 equations with 8 unknowns: 

     
x1^2 + x2^2 -1=0
x3^2 + x4^2 -1=0
x5^2 + x6^2 -1=0
x7^2 + x8^2 -1=0
0.004731*x1*x3-0.3578*x2*x3-0.1238*x1-0.001637*x2-0.9338*x4+x7 - 0.3571=0
0.2238*x1*x3+0.7623*x2*x3+0.2638*x1-0.07745*x2-0.6734*x4-0.6022 =0
x6*x8+0.3578*x1+0.004731*x2 =0
0.2238*x2-0.7623*x1+0.3461 =0
    Ranges: [-1,1] for all unknowns

    Solving method: GradientSolve+HullConsistencyStrong+ +3B
    Solutions:: 16 (exact)
    Computation time (May 2004):

    DELL D400 (1.7GHz) 0.23s

    Kincox

    Origin: COCONUT
    4 equations with 4 unknowns with a =1, b=4, l1=10, l2=6 

     
 -a + l2*(c1*c2 - s1*s2) + l1*c1=0
 -b + l2*(c1*s2 + c2*s1) + l1*s1=0
 c1^2 + s1^2 - 1=0
 c2^2 + s2^2 - 1=0
    Ranges: [-1,1] for all unknowns

    Solving method: GradientSolve+HullConsistencyStrong+ +3B
    Solutions:: 2 (exact)
    Computation time (May 2004):

    DELL D400 (1.7GHz) 0.01s
    See also the non-algebraic version of this problem

    More 10/80

    Origin: COCONUT
    10 equations with 10 unknowns (or 80 equations with 80 unknowns) 

    X1+.3756574005e-2*(X1+1.090909091)^3+.3380916604e-2*(X2+1.181818182)^3
+.3005259204e-2*(X3+1.272727273)^3+.2629601803e-2*(X4+1.363636364)^3
+.2253944403e-2*(X5+1.454545455)^3+.1878287002e-2*(X6+1.545454545)^3
+.1502629602e-2*(X7+1.636363636)^3+.1126972201e-2*(X8+1.727272727)^3
+.7513148009e-3*(X9+1.818181818)^3+.3756574005e-3*(X10+1.909090909)^3=0

 X2+.3380916604e-2*(X1+1.090909091)^3+.6761833208e-2*(X2+1.181818182)^3
+.6010518407e-2*(X3+1.272727273)^3+.5259203606e-2*(X4+1.363636364)^3
+.4507888805e-2*(X5+1.454545455)^3+.3756574005e-2*(X6+1.545454545)^3
+.3005259204e-2*(X7+1.636363636)^3+.2253944403e-2*(X8+1.727272727)^3
+.1502629602e-2*(X9+1.818181818)^3+.7513148009e-3*(X10+1.909090909)^3=0

 X3+.3005259204e-2*(X1+1.090909091)^3+.6010518407e-2*(X2+1.181818182)^3
+.9015777611e-2*(X3+1.272727273)^3+.7888805409e-2*(X4+1.363636364)^3
+.6761833208e-2*(X5+1.454545455)^3+.5634861007e-2*(X6+1.545454545)^3
+.4507888805e-2*(X7+1.636363636)^3+.3380916604e-2*(X8+1.727272727)^3
+.2253944403e-2*(X9+1.818181818)^3+.1126972201e-2*(X10+1.909090909)^3=0

 X4+.2629601803e-2*(X1+1.090909091)^3+.5259203606e-2*(X2+1.181818182)^3
+.7888805409e-2*(X3+1.272727273)^3+.1051840721e-1*(X4+1.363636364)^3
+.9015777611e-2*(X5+1.454545455)^3+.7513148009e-2*(X6+1.545454545)^3
+.6010518407e-2*(X7+1.636363636)^3+.4507888805e-2*(X8+1.727272727)^3
+.3005259204e-2*(X9+1.818181818)^3+.1502629602e-2*(X10+1.909090909)^3=0

 X5+.2253944403e-2*(X1+1.090909091)^3+.4507888805e-2*(X2+1.181818182)^3
+.6761833208e-2*(X3+1.272727273)^3+.9015777611e-2*(X4+1.363636364)^3
+.1126972201e-1*(X5+1.454545455)^3+.9391435011e-2*(X6+1.545454545)^3
+.7513148009e-2*(X7+1.636363636)^3+.5634861007e-2*(X8+1.727272727)^3
+.3756574005e-2*(X9+1.818181818)^3+.1878287002e-2*(X10+1.909090909)^3=0

 X6+.1878287002e-2*(X1+1.090909091)^3+.3756574005e-2*(X2+1.181818182)^3
+.5634861007e-2*(X3+1.272727273)^3+.7513148009e-2*(X4+1.363636364)^3
+.9391435011e-2*(X5+1.454545455)^3+.1126972201e-1*(X6+1.545454545)^3
+.9015777611e-2*(X7+1.636363636)^3+.6761833208e-2*(X8+1.727272727)^3
+.4507888805e-2*(X9+1.818181818)^3+.2253944403e-2*(X10+1.909090909)^3=0

 X7+.1502629602e-2*(X1+1.090909091)^3+.3005259204e-2*(X2+1.181818182)^3
+.4507888805e-2*(X3+1.272727273)^3+.6010518407e-2*(X4+1.363636364)^3
+.7513148009e-2*(X5+1.454545455)^3+.9015777611e-2*(X6+1.545454545)^3
+.1051840721e-1*(X7+1.636363636)^3+.7888805409e-2*(X8+1.727272727)^3
+.5259203606e-2*(X9+1.818181818)^3+.2629601803e-2*(X10+1.909090909)^3=0

 X8+.1126972201e-2*(X1+1.090909091)^3+.2253944403e-2*(X2+1.181818182)^3
+.3380916604e-2*(X3+1.272727273)^3+.4507888805e-2*(X4+1.363636364)^3
+.5634861007e-2*(X5+1.454545455)^3+.6761833208e-2*(X6+1.545454545)^3
+.7888805409e-2*(X7+1.636363636)^3+.9015777611e-2*(X8+1.727272727)^3
+.6010518407e-2*(X9+1.818181818)^3+.3005259204e-2*(X10+1.909090909)^3=0

 X9+.7513148009e-3*(X1+1.090909091)^3+.1502629602e-2*(X2+1.181818182)^3
+.2253944403e-2*(X3+1.272727273)^3+.3005259204e-2*(X4+1.363636364)^3
+.3756574005e-2*(X5+1.454545455)^3+.4507888805e-2*(X6+1.545454545)^3
+.5259203606e-2*(X7+1.636363636)^3+.6010518407e-2*(X8+1.727272727)^3
+.6761833208e-2*(X9+1.818181818)^3+.3380916604e-2*(X10+1.909090909)^3=0

 X10+.3756574005e-3*(X1+1.090909091)^3+.7513148009e-3*(X2+1.181818182)^3
+.1126972201e-2*(X3+1.272727273)^3+.1502629602e-2*(X4+1.363636364)^3
+.1878287002e-2*(X5+1.454545455)^3+.2253944403e-2*(X6+1.545454545)^3
+.2629601803e-2*(X7+1.636363636)^3+.3005259204e-2*(X8+1.727272727)^3
+.3380916604e-2*(X9+1.818181818)^3+.3756574005e-2*(X10+1.909090909)^3=0
    Ranges: [-1e8,0] for all unknowns

    Solving method: GradientSolve+HullConsistencyStrong+ +3B
    Solutions:: 1 (exact)
    Computation time (May 2004):

    DELL D400 (1.7GHz) 0.02s (10 equations), 437s (80 equations)

    Nauheim

    Origin: COCONUT
    8 equations with 8 unknowns 

     
e*g + 2*d*h =0
9*e + 4*b =0
4*c*h + 2*e*f + 3*d*g =0
7*c - 9*a + 8*f =0
4*d*f + 5*c*g + 6*h + 3*e =0
5*d + 6*c*f + 7*g - 9*b =0
9*d + 6*a - 5*b=0
-9*c + 7*a - 8=0
    Ranges: [-1e8,1e8] for all unknowns

    Solving method: GradientSolve+HullConsistencyStrong+ +3B
    Solutions:: 4 (exact)
    Computation time (May 2004):

    DELL D400 (1.7GHz) 0.62s

    Neveu1

    Origin: COPRIN
    Physical meaning: we consider a set of points in a plane. Among these points the distance between some pairs is known
    26 equations

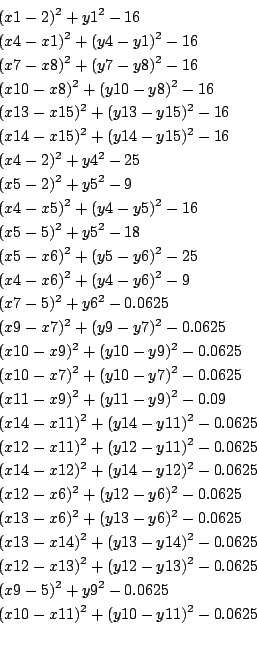
    \begin{eqnarray*} &&(x1-2)^{2}+{y1}^{2}-16\\ &&(x4-x1)^{2}+(y4-y1)^{2}-16\\ &&... ...{2}+{y9}^{2}- 0.0625\\ &&(x10-x11)^{2}+(y10-y11)^{2}- 0.0625\\ \end{eqnarray*}

    (x1-2)^{2}+{y1}^{2}-16=0
(x4-x1)^{2}+(y4-y1)^{2}-16=0
(x7-x8)^{2}+(y7-y8)^{2}-16=0
(x10-x8)^{2}+(y10-y8)^{2}-16=0
(x13-x15)^{2}+(y13-y15)^{2}-16=0
(x14-x15)^{2}+(y14-y15)^{2}-16=0
(x4-2)^{2}+{y4}^{2}-25=0
(x5-2)^{2}+{y5}^{2}-9=0
(x4-x5)^{2}+(y4-y5)^{2}-16=0
(x5-5)^{2}+{y5}^{2}-18=0
(x5-x6)^{2}+(y5-y6)^{2}-25=0
(x4-x6)^{2}+(y4-y6)^{2}-9=0
(x7-5)^{2}+{y6}^{2}- 0.0625=0
(x9-x7)^{2}+(y9-y7)^{2}- 0.0625=0
(x10-x9)^{2}+(y10-y9)^{2}- 0.0625=0
(x10-x7)^{2}+(y10-y7)^{2}- 0.0625=0
(x11-x9)^{2}+(y11-y9)^{2}- 0.09=0
(x14-x11)^{2}+(y14-y11)^{2}- 0.0625=0
(x12-x11)^{2}+(y12-y11)^{2}- 0.0625=0
(x14-x12)^{2}+(y14-y12)^{2}- 0.0625=0
(x12-x6)^{2}+(y12-y6)^{2}- 0.0625=0
(x13-x6)^{2}+(y13-y6)^{2}- 0.0625=0
(x13-x14)^{2}+(y13-y14)^{2}- 0.0625=0
(x12-x13)^{2}+(y12-y13)^{2}- 0.0625=0
(x9-5)^{2}+{y9}^{2}- 0.0625=0
(x10-x11)^{2}+(y10-y11)^{2}- 0.0625=0
    Unknowns:
    x1,y1,x4,y4,x5,y5,x6,y6,x7,y7,x8,y8,x9,y9,x10,y10,x11,y11,x12,y12, x13,y13,x14,y14,x15,y15

    Range: may be chosen arbitrary large without any change in the computation time
    Solving method: SolveDistance
    Solutions:: 128 (exact)
    Computation time (April 2003):

    EVO 410C (1.2Ghz) 437.8s

    Piano

    Origin: COCONUT
    9 equations with 9 unknowns 

     
x - l*t^3 - L*w =0
y - L*t - l*w^3 =0
L - 1           =0
l - 2           =0
x - a           =0
2*a - 3         =0
y - b           =0
b - r*t         =0
w^2 - 1 + t^2   =0
    Ranges: [-100000,100000] for all unknowns except w [0,100000]

    Solving method: GradientSolve+HullConsistencyStrong+ +3B
    Solutions:: 1 (exact)
    Computation time (May 2004):

    DELL D400 (1.7GHz) 0.01s

    Pramanik

    Origin: Pramanik [10]
    Physical meaning: the unknowns are geometrical parameters of a car steering mechanism. The purpose of the system is to determine the possible mechanisms such that the trajectory followed by the mechanism goes through pre-defined points

    Let $E,F$ be defined as:

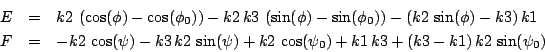
    \begin{eqnarray*} E&=&k2 \left (\cos(\phi)-\cos(\phi_0)\right )-k2 k3 \left (... ...i)+k2 \cos(\psi_0)+k1 k3+\left (k3-k1\right )k2 \sin(\psi_0) \end{eqnarray*}

    and the equation:

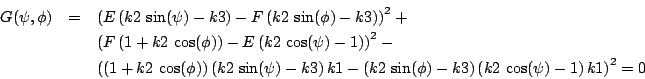
    \begin{eqnarray*} G(\psi,\phi)&=&\left (E\left (k2 \sin(\psi)-k3\right )-F\left... ...n(\phi)-k3\right )\left (k2 \cos(\psi)-1\right )k1\right )^2=0 \end{eqnarray*}

    Let:

    \begin{displaymath} \psi_0=1.3954170041747090114   \phi_0=1.7461756494150842271 \end{displaymath}

    and

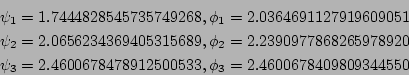
    \begin{eqnarray*} &&\psi_1=1.7444828545735749268, \phi_1=2.0364691127919609051\\... ...\ &&\psi_3= 2.4600678478912500533, \phi_3=2.4600678409809344550 \end{eqnarray*}

    A system of 3 equations is obtained with $G(\psi_i,\phi_i)$ for i in [1,3]

    Unknowns:k1,k2,k3

    Ranges: [0.06,1] for all unknowns

    Solving method: HessianSolve
    Solutions:: 2 (exact)
    Computation time (April 2003):

    Sun Blade 31.31s
    EVO 410C (1.2Ghz) 12.58s

    Prolog

    Origin: Norton, R D, and Scandizzo, P L, Market Equilibrium Computations in Activity Analysis Models. Operations Research 29, 2 (1981)
    23 equations in 21 unknowns, x1,..x21
    Ranges for the unknowns: [-1e8,1e8] for x1, [0.2,1e8] for x2,x3,x4, [0,1e8] for the other variables 

    x5 + x6 - 0.94*x11 - 0.94*x12 - 0.94*x13 + 0.244*x17 + 0.244*x18+ 0.244*x19 =0

  0.064*x11 + 0.064*x12 + 0.064*x13 - 0.58*x14 - 0.58*x15 - 0.58*x16
      + 0.172*x17 + 0.172*x18 + 0.172*x19 =0

  x7 + x8 + 0.048*x11 + 0.048*x12 + 0.048*x13 + 0.247*x14 + 0.247*x15
      + 0.247*x16 - 0.916*x17 - 0.916*x18 - 0.916*x19 =0

  x11 + 1.2*x12 + 0.8*x13 + 2*x14 + 1.8*x15 + 2.4*x16 + 3*x17 + 2.7*x18
      + 3.2*x19 - 3712=0

  2*x11 + 1.8*x12 + 2.2*x13 + 3*x14 + 3.5*x15 + 2.3*x16 + 3*x17 + 3.2*x18
      + 2.7*x19 - 5000=0

356.474947137148*x2 + 53.7083537310174*x4 + x5 - 0.564264890180399*x20- 352=0

339.983422262764*x2 + 43.5418249774113*x4 + x6 - 0.405939876920766*x21- 430=0

106.946746119538*x2 + 145.018955433089*x4 + x7 - 0.507117039797071*x20 - 222=0

173.929713444361*x2 + 203.031384299627*x4 + x8 - 0.578889145413521*x21 - 292=0

x5*x2 + x7*x4 - x20 =0

x6*x2 + x8*x4 - x21 =0

 - 3340.8*x9 - 500*x10 + x20 =0

 - 371.2*x9 - 4500*x10 + x21 =0

   0.94*x2 - 0.064*x3 - 0.048*x4 - x9 - 2*x10 =0

   0.94*x2 - 0.064*x3 - 0.048*x4 - 1.2*x9 - 1.8*x10 =0

   0.94*x2 - 0.064*x3 - 0.048*x4 - 0.8*x9 - 2.2*x10 =0

   0.58*x3 - 0.247*x4 - 2*x9 - 3*x10 =0

   0.58*x3 - 0.247*x4 - 1.8*x9 - 3.5*x10 =0

   0.58*x3 - 0.247*x4 - 2.4*x9 - 2.3*x10 =0

 - 0.244*x2 - 0.172*x3 + 0.916*x4 - 3*x9 - 3*x10 =0

 - 0.244*x2 - 0.172*x3 + 0.916*x4 - 2.7*x9 - 3.2*x10 =0

 - 0.244*x2 - 0.172*x3 + 0.916*x4 - 3.2*x9 - 2.7*x10 =0

 - (x5*x2 + x6*x2 + x7*x4 + x8*x4) - x1 + 3712*x9 + 5000*x10 =0
    Solving method: GradientSolve+HullConsistency+ +3B
    Solutions:: 0
    Computation time (September 2004):
    DELL D400 (1.7GHz) 16.73s

    Puma

    Origin: COCONUT
    Physical meaning: inverse kinematics of a 3R robot
    8 equations with 8 unknowns 

     
x1^2 + x2^2 - 1 =0
x3^2 + x4^2 - 1 =0
x5^2 + x6^2 - 1 =0
x7^2 + x8^2 - 1 =0
0.004731*x1*x3 - 0.3578*x2*x3 - 0.1238*x1 - 0.001637*x2 - 0.9338*x4 + x7=0
1 =0
0.2238*x1*x3 + 0.7623*x2*x3 + 0.2638*x1 - 0.07745*x2 -0.6734*x4 -0.6022 =0
x6*x8 + 0.3578*x1 + 0.004731*x2 =0
-0.7623*x1 + 0.2238*x2 + 0.3461 =0
    Ranges: [-1,1] for all unknowns

    Solving method: GradientSolve+HullConsistencyStrong+ +3B
    Solutions:: 16 (exact)
    Computation time (May 2004):

    DELL D400 (1.7GHz) 0.23s
    See also the modified puma bench

    Redeco8

    Origin: COCONUT
    8 equations with 8 unknowns 

     
x1 + x1*x2 + x2*x3 + x3*x4 + x4*x5 + x5*x6 + x6*x7 - 1*u8 =0
        x2 + x1*x3 + x2*x4 + x3*x5 + x4*x6 + x5*x7 - 2*u8 =0
                x3 + x1*x4 + x2*x5 + x3*x6 + x4*x7 - 3*u8 =0
                        x4 + x1*x5 + x2*x6 + x3*x7 - 4*u8 =0
                                x5 + x1*x6 + x2*x7 - 5*u8 =0
                                        x6 + x1*x7 - 6*u8 =0
                                                x7 - 7*u8 =0
                     x1 + x2 + x3 + x4 + x5 + x6 + x7 + 1 =0
    Ranges: [-1e8,1e8] for all unknowns

    Solving method: GradientSolve+HullConsistencyStrong+ +3B
    Solutions:: 8 (exact)
    Computation time (May 2004):

    DELL D400 (1.7GHz) 39.46s

    Robot kinematics

    Origin: [6]
    Physical meaning: find the joint angles of a 4 degrees-of-freedom robot for reaching a given pose with the end-effector
    8 equations

    \begin{eqnarray*} &&- 0.1238 x_1+x_7- 0.001637 x_2- 0.9338 x_4+ 0.004731 x_1 x_3... ...^2-1\\ &&x_3^2+x_4^2-1\\ &&x_5^2+x_6^2-1\\ &&x_7^2+x_8^2-1\\ \end{eqnarray*}

     
- 0.1238 x_1+x_7- 0.001637 x_2- 0.9338 x_4+ 0.004731 x_1 x_3- 0.3578 x_2 x_3- 0.3571
 0.2638 x_1-x_7- 0.07745 x_2- 0.6734 x_4+ 0.2238 x_1 x_3+ 0.7623 x_2 x_3- 0.6022
 0.3578 x_1+ 0.004731 x_2+x_6 x_8- 0.7623 x_1+ 0.2238 x_2+ 0.3461
x_1^2+x_2^2-1
x_3^2+x_4^2-1
x_5^2+x_6^2-1
x_7^2+x_8^2-1
    Ranges: for all unknowns [-1,1]

    Solving method: HessianSolve+HullConsistency+ SimplexConsistency+3B
    Solutions:: 16 (exact)
    Computation time (April 2003):

    Evo 410C (1.2Ghz) 0.38s

    Rose

    Origin: COCONUT, Shoven :"Applied general equilibrium modelling", IMF Staff Papers, pages 394-419, 1983
    Physical meaning: a general economic equilibrium model

    3 equations defined by: 

     
y^4-20/7*x^2 =0

x^2*z^4+7/10*x*z^4+7/48*z^4-50/27*x^2-35/27*x-49/216 =0

3/5*x^6*y^2*z+x^5*y^3+3/7*x^5*y^2*z+7/5*x^4*y^3-7/20*x^4*y*z^2-
   3/20*x^4*z^3+609/1000*x^3*y^3+63/200*x^3*y^2*z-77/125*x^3*y*z^2-
   21/50*x^3*z^3+49/1250*x^2*y^3+147/2000*x^2*y^2*z-
   23863/60000*x^2*y*z^2-91/400*x^2*z^3-27391/800000*x*y^3+
   4137/800000*x*y^2*z-1078/9375*x*y*z^2-5887/200000*x*z^3-1029/160000*y^3-
   24353/1920000*y*z^2-343/128000*z^3 =0
    Ranges: for all unknowns [-1e8,1e8]

    Solving method: GradientSolve+HullConsistencyStrong+3B
    Solutions:: 16 (exact) +2 singular
    Computation time (May 2004)

    DELL D400 (1.7 GHz) 2.87s

    6body

    Origin: FRISCO
    Physical meaning: Polynomial systems arising in the study of central configurations in the N-body problem of Celestial Mechanics
    6 equations

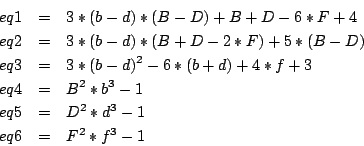
    \begin{eqnarray*} eq1&=&3*(b-d)*(B-D)+B+D-6*F+4\\ eq2&=&3*(b-d)*(B+D-2*F)+5*(B-... ...)+4*f+3\\ eq4&=&B^2*b^3-1\\ eq5&=&D^2*d^3-1\\ eq6&=&F^2*f^3-1 \end{eqnarray*}

    3*(b-d)*(B-D)+B+D-6*F+4=0
3*(b-d)*(B+D-2*F)+5*(B-D)=0
3*(b-d)^2-6*(b+d)+4*f+3=0
B^2*b^3-1=0
D^2*d^3-1=0
F^2*f^3-1=0
    Ranges: for all unknowns [0,1e5]
    Solving method: HessianSolve+HullConsistencyStrong+0.95
    Solutions:: 5 (exact)
    Computation time:
    Sun Blade 28.69s (April 2003)
    EVO 410C (1.2Ghz) 4.68s (April 2003)
    DELL D400 (1.7Ghz) 0.95s (May 2004)

    Stenger

    Origin: [7]
    2 equations:

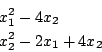
    \begin{eqnarray*} &&x_1^2-4 x_2\\ &&x_2^2-2x_1+4x_2 \end{eqnarray*}

    Ranges: [-1e8,1e8]

    Solving method: HessianSolve+HullConsistency+ 3B
    Solutions:: 2 (exact)
    Computation time

    DELL 620 (May 2007) (1.7GHz) 0.01s

    Yamamura1

    Origin: Yamamura [15]
    n equations defined by:

    \begin{displaymath} 2.5x_i^3-10.5x_i^2+11.8x_i-i+\sum_{i =1}^{i =n}x_i =0  i \in [1,n] \end{displaymath}

    solved here for n=16,32

    Ranges: for all unknowns [-1e8,1e8]

    Solving method: SolveSimplexGradient+HullConsistency+3B
    Solutions:: 9 for n=16, 7 for n=32 (exact)
    Computation time (April 2003):

    Sun Blade 2.11s
    EVO 410C (1.2Ghz) 39.25s (n=16), 975s (n=32)

    next up previous Next: Non-polynomial systems Up: benches Previous: benches
  • La page de J-P. Merlet
  • J-P. Merlet home page
  • La page Présentation de COPRIN
  • COPRIN home page
  • La page "Présentation" de l'INRIA
  • INRIA home page

    Jean-Pierre Merlet