



Next: The WeylFilter procedure
Up: Simplification procedures
Previous: Routh table: Routh
Contents
The KharitonovConsistency procedure
This procedure may be used when dealing with the problem of determining
if the roots of a parametric polynomial all lie within a given range.
For a parametric polynomial there is usually four Kharitonov
polynomials i.e. polynomials have that have constant
coefficients. It can be shown that if all the Kharitonov polynomials have
the real parts of their roots of the same sign, then all the
polynomials in the set will have the real part of their of the same
sign. The following procedure allows to use the Kharitonov polynomials
to test if there they may be roots of a parametric polynomial within a
given range.
Its syntax is:
KharitonovConsistency(Func,Vars,Gradient,procname)
with the following parameters:
- Func: a polynomial. If Func is a matrix, then the
polynomial is supposed to be the characteristic polynomial of the
matrix
- Vars: list of unknowns. The first one must be the unknown of the
polynomial. If Func is a matrix the first name must be
AXX
- Gradient: a flag that indicates if the derivatives of the
polynomial with respect to the unknowns may be used (1) or not (0)
- procname: the name of the simplification procedure. The name of
the created file will be procname.C
This procedure will calculate for the polynomial 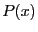 the
coefficients of the polynomial
the
coefficients of the polynomial 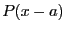 . Then the simplification
procedure will consider that its input box has as first element a range
for
. Then the simplification
procedure will consider that its input box has as first element a range
for 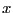 and update
and update 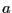 so that the Kharitonov polynomial will
indicate if the polynomial may have a root larger than the lower bound
of the first element of the box or lower than the upper bound of this
interval. This procedure is intended to be used in conjunction with
the procedure dealing with parametric polynomials.
so that the Kharitonov polynomial will
indicate if the polynomial may have a root larger than the lower bound
of the first element of the box or lower than the upper bound of this
interval. This procedure is intended to be used in conjunction with
the procedure dealing with parametric polynomials.




Next: The WeylFilter procedure
Up: Simplification procedures
Previous: Routh table: Routh
Contents
Jean-Pierre Merlet
2012-12-20