



Next: The KharitonovConsistency procedure
Up: Simplification procedures
Previous: Simplification procedures
Contents
The Routh table allows one to determine if all the roots of a polynomial
have a negative real part. The number of sign changes in the first column
of the table is the number of roots with positive real parts.
The Routh table has n+1 rows, where n
is the degree of the polynomial.
The syntax of this procedure is:
Routh(poly,Vars,Type,Where,ProcName)
where:
- poly is the polynomial
- Vars: a list of variable name whose first element is the
polynomial variable
- Type: see below
- Where: if P(x) is the polynomial we will compute the Routh table
for P(x+Where). If Where
is not 0 the number of sign changes will indicate the number of roots
with real part greater than Where.
- ProcName: the name of the simplification procedure
Type allows to control the output of this procedure:
- 0 : the procedure will simply returns the Routh table of the
polynomial
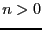 and lower than the degree of the polynomial +1 : the
procedure will create a C++ simplification procedure (whose name is
the last argument of the procedure) that
will compute an interval evaluation of the
and lower than the degree of the polynomial +1 : the
procedure will create a C++ simplification procedure (whose name is
the last argument of the procedure) that
will compute an interval evaluation of the 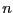 first element of
the first column of the Routh table, using the derivatives of these
elements. This simplification procedure will return -1 if the
polynomial has a root with real part larger than Where. The interval
input of this procedure will be an interval vector corresponding to
Vars. Note that if
first element of
the first column of the Routh table, using the derivatives of these
elements. This simplification procedure will return -1 if the
polynomial has a root with real part larger than Where. The interval
input of this procedure will be an interval vector corresponding to
Vars. Note that if 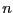 is large the procedure may take a long time
to be generated.
is large the procedure may take a long time
to be generated.
-
![$[k,[n,var1,var2..],[m,var3]]$](img164.png) : if
: if 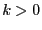 the same
simplification principle
than described in the above section will be generated. Furthermore
we will calculate the sign of the first element of the first row
of the Routh table. If this element has a constant sign (say positive)
we will consider the element at the n-th row of the first column.
Assuming that this element S has a linear term in var1 (S= a var1+b)
with a positive we will write that S is positive when var1
is greater than -b/a and we will update var1
accordingly.
We will proceed similarly with the element at of row m and with
variable var3
the same
simplification principle
than described in the above section will be generated. Furthermore
we will calculate the sign of the first element of the first row
of the Routh table. If this element has a constant sign (say positive)
we will consider the element at the n-th row of the first column.
Assuming that this element S has a linear term in var1 (S= a var1+b)
with a positive we will write that S is positive when var1
is greater than -b/a and we will update var1
accordingly.
We will proceed similarly with the element at of row m and with
variable var3
Consider the polynomial
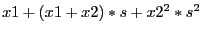 in the variable
in the variable
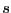 . Its Routh table at 0 is:
. Its Routh table at 0 is:
Routh(x1+(x1+x2)*s+x2^2*s^2,[s,x1,x2],0,0);
[ 2 ]
[ x2 x1 0]
[ ]
[x1 + x2 0 0]
[ ]
[ x1 0 0]
The first element of the Routh table is positive and
the second element of the first row is 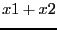 . Hence a necessary
condition for the polynomial for not having root with real part
positive is that
. Hence a necessary
condition for the polynomial for not having root with real part
positive is that 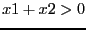 . Hence writing:
. Hence writing:
Routh(x1+(x1+x2)*s+x2^2*s^2,[s,x1,x2],[2,[2,x1,x2]],0,"ROUTH");
will imply that the simplification procedure will use the
simplification rules 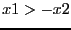 and
and 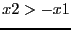 . If x1=[-5,5] and x2=[0,4]
. If x1=[-5,5] and x2=[0,4]
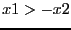 will imply
will imply ![$[-5,5]>[-4,0]$](img172.png) which leads to the new range [-4,5]
for
which leads to the new range [-4,5]
for 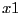




Next: The KharitonovConsistency procedure
Up: Simplification procedures
Previous: Simplification procedures
Contents
Jean-Pierre Merlet
2012-12-20