The WeylFilter procedure

Let $P$ be a polynomial and be maxroot the maximal modulus of the root of $P$. From $P$ we may derive a the unitary polynomial $Q$ such that the roots of $Q$ have a modulus lower or equal to 1 and if $w$ is a root of $Q$ then maxroot$w$ is a root of $P$.

Let $Q=sum_{i=0}^{i=n} a_i x^i$ which may also be written as $sum_{i=0}^{i=n} b_i(x-a)^i$ where $a$ is some fixed point.

Let a range $[a,b]$ for $x$ and let $z_0$ be the mid point of the range. We consider the square in the complex plane centered at $z_0$ and whose edge length is $b-a$. Let $\delta$ be the length of the half-diagonal of this square. If

$$\vert b_0\vert> \sum_{j=1}^{j=n} \vert b_j\vert\delta^j$$

then the polynomial has no root in the square. For a given list of equations we consider in turn each equation and determine if it may be considered as a parametric polynomial. For example the equation $x^2\sin(x)+x\sin(y)+ x exp(x)$ will be considered as a second order polynomial in $x$ with coefficients $\sin(x), \sin(y)+exp(x)$ (but not a polynomial in $y$). The procedure

 
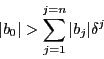
WeylFilter(Func,Vars,FullVars,MaxRoot,TypeB,name)

will consider each equation in the list Func and examine if it may considered as a parametric polynomial successively in each variable in the list Vars. If yes the Weyl filter will be used on the polynomial whose coefficients are functions of the variables in the list FullVars (all variables in Vars must be a member of FullVars). MaxRoot is a list which indicates for each variable in Vars what is the maximum modulus of the roots of all parametric polynomials in this variable. An element of MaxRoot may be a numerical value of the key-word "automatic" which indicates that the C++ program will try to determine the maximal modulus. The list TypeB indicates for each variable in Vars how are computed the $b_i$ i.e. numerically with the keyword "numeric", or symbolically (which is usually more efficient) with the keyword "symbolic". The simplification procedure will be named name and be written in the file name.C. For the previous example the procedure will be

 
WeylFilter([x^2*sin(x)+x*sin(y)+ x*exp(x)],[x],[x,y],["automatic"],["symbolic"],"SIMP");

Another example of the use of this procedure is presented in section 12.3.