Implementation

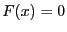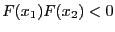Brent's method enable to find a root of an equation $F(x)=0$ as soon as the root is bracketed in an interval $[x_1,x_2]$ such that $F(x_1)F(x_2)<0$. It is implemented as:

 
int Brent(REAL (* TheFunction)(REAL),INTERVAL &Input,
      double AccuracyV,double Accuracy,int Max_Iter,double *Sol, double *Residu)

with:

• TheFunction: a procedure which enable to compute the value of the equation at a given point
• Input: the interval $[x_1,x_2]$ in which we are looking for a root
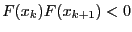• AccuracyF: a threshold on the minimal value of the width of the interval $[x_k, x_{k+1}]$ with $F(x_k)F(x_{k+1})<0$ considered during the procedure
• Accuracy: a threshold on the value of 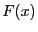$F(x)$ which determine a root of the equation
• MaxIter: maximal number of iteration
• Sol: on success the value of the root
• Residu: the value of the equation at Sol

The procedure returns:

• 1: a solution has been found as F(Sol)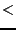$<$Accuracy
• 2: a solution has been found as 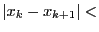$\vert x_k-x_{k+1}\vert<$AccuracyV
• -1: $F(x_1)F(x_2)>0$
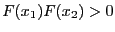
• -3: the maximal number of iteration has been reached without finding a solution

The test program Test_Ridder2 present a program to solve the trigonometric equation presented as example 2 (see section 15.1.1).