



Next: Implementation
Up: Brent method for solving
Previous: Brent method for solving
Contents
Brent method is an iterative scheme used to obtain one root of the
equation 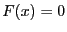 within an interval
within an interval ![$[x_1,x_2]$](img278.png) . It assumes that
. It assumes that
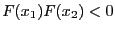 . Let
. Let 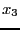 be the mid-point of the interval
be the mid-point of the interval
![$[x_1,x_2]$](img278.png) . A new estimate of the root is
. A new estimate of the root is 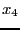 with:
with:
with:
In this method 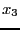 is considered to be the current estimate of the
solution. The term
is considered to be the current estimate of the
solution. The term 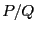 is a correction factor: when this factor
leads to a new estimate of the solution outside the interval we use a
bisection method to compute a new interval
is a correction factor: when this factor
leads to a new estimate of the solution outside the interval we use a
bisection method to compute a new interval ![$[x_1,x_2]$](img278.png) . In other words
if
. In other words
if
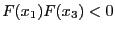 the new interval is
the new interval is ![$[x_1,x_3]$](img297.png) and if
and if
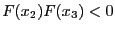 the new interval is
the new interval is ![$[x_3,x_2]$](img299.png) . Therefore Brent
method is a cross between a bisection method and a super-linear method
which insure that the estimate of the solution always lie within the
interval
. Therefore Brent
method is a cross between a bisection method and a super-linear method
which insure that the estimate of the solution always lie within the
interval ![$[x_1,x_2]$](img278.png) .
.
Jean-Pierre Merlet
2012-12-20
![\begin{eqnarray*}
R&=&
\frac{F(x_3)}{F(x_2)}~~~~S=\frac{F(X_3)}{F(x_1)}~~~~~T=\f...
...\\
P&=&S[T(R-T)(x_2-x_3)-(1-R)(x_3-x_1)]\\
Q&=&(T-1)(R-1)(S-1)
\end{eqnarray*}](img294.png)