



Next: Implementation
Up: Mathematical background
Previous: Improving the evaluation using
Contents
Single bisection mode
We may use the single bisection mode i.e. bisect only one variable at
a time. Fives modes exist for determining the variable to be bisected,
the choice being made by setting Single_Bisection to a value
from 1 to 8
- 1 : we just split the variable having
the largest width
- 2 : this mode is based on the smear function
as defined by
Kearfott [7]: let
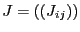 be the Jacobian
matrix of the system and let define for the variable
be the Jacobian
matrix of the system and let define for the variable 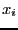 the
smear value
the
smear value
![$s_i = {\rm Max}(
\vert\underline{J_{ij}[\underline{x_i},\overline{x_i}]}\vert,
\vert\overline{J_{ij}[\underline{x_i},\overline{x_i}]}\vert$](img238.png)
![$\forall j\in
[1,n]$](img239.png) where
where  is the total number of functions. The variable that
will be bisected will be the one having the largest
is the total number of functions. The variable that
will be bisected will be the one having the largest 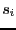 .
There is however a drawback f the smear function: let consider for
example the equation
.
There is however a drawback f the smear function: let consider for
example the equation 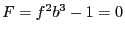 where
where 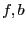 are large identical
intervals centered at 0.
The derivative of
are large identical
intervals centered at 0.
The derivative of 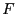 with respect to
with respect to 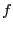 is
is 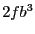 and
with respect to
and
with respect to 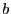
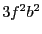 : multiplied by the width of the interval
we get
: multiplied by the width of the interval
we get 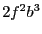 and
and 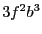 . Hence the smear function for
. Hence the smear function for 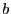 will
be in general larger than for
will
be in general larger than for 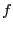 and
and 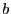 will always be bisected until its
width is lower than the desired accuracy. Another example in which the
smear function is not the best choice is presented in
section 2.4.3.4.
However the smear function is very often the most efficient mode and
should be privileged.
will always be bisected until its
width is lower than the desired accuracy. Another example in which the
smear function is not the best choice is presented in
section 2.4.3.4.
However the smear function is very often the most efficient mode and
should be privileged.
- 3 : this is similar to the smear function except that we take
into account its drawback. To avoid bisecting over and over the same
variable we impose that a variable may be considered for bisection
only if the ratio of its width over the maximal width of the box
is not lower than the variable ALIAS_Bound_Smear
(default value 1.e-5).
- 4 : this mode is based on the Krawczyk operator:
to determine which variable should be bisected we
consider the box
![$P=\{[\underline{x_1},\overline{x_1}],\ldots,
[\underline{x_n},\overline{x_n}]\}$](img248.png) . When dealing with the variable
. When dealing with the variable
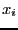 the single bisection mode will lead to two new boxes
the single bisection mode will lead to two new boxes
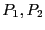 . Let
. Let 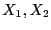 be the middle point of these boxes
We have seen (section 2.10) that a fundamental point
of Moore test
for determining the unicity of a solution in a box is
that
be the middle point of these boxes
We have seen (section 2.10) that a fundamental point
of Moore test
for determining the unicity of a solution in a box is
that
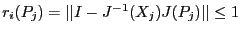 . Thus we will consider in turn
each of the variable and compute the value of
. Thus we will consider in turn
each of the variable and compute the value of 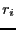 for both
for both 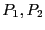 . The bisected variable will be chosen as the one leading to the
minimal value of all
. The bisected variable will be chosen as the one leading to the
minimal value of all 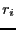 . However to avoid bisecting over and over
the same variable we use another test: let
. However to avoid bisecting over and over
the same variable we use another test: let 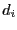 be the width of the
interval
be the width of the
interval
![$[\underline{x_i},\overline{x_i}]$](img116.png) and
and 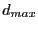 be the
maximum of all the
be the
maximum of all the 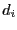 . If
. If
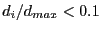 we don't consider the
variable
we don't consider the
variable 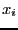 as a possible bisection direction.
as a possible bisection direction.
- 5: we use a round-robin mode i.e. each variable is
bisected in turn (first
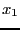 , then
, then 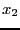 and so on) unless the width
of the range for the variable is less than the desired accuracy on the
variable, in which case the bisected variable is the next one having a
sufficient width
and so on) unless the width
of the range for the variable is less than the desired accuracy on the
variable, in which case the bisected variable is the next one having a
sufficient width
- 6: like mode 2 of SolveGeneral. ALIAS_RANDG may
still be used to switch between mode 1 and mode 2 of SolveGeneral
- 7: like mode 2 of SolveGeneral except that it is assumed
that the user has defined a simplification procedure that may allow to
reduce the box directly within the bisection process
- 8: the variable are regrouped by groups of
ALIAS_Tranche_Bisection elements. The bisection will look at
each group in turn and bisect the first group that has elements whose
diameter is larger than ALIAS_Size_Tranche_Bisection. When
the element of the group have all elements whose diameter is lower
than this threshold the bisection will consider the next group. If all
elements of all groups have a diameter lower than the threshold the
smear function will be used to determine which variable will be
bisected.
The smear mode leads in general to better result
than the other modes (but there are exception, see example in
section 2.4.3.4).
There is another mode called the mixed bisection: among the  variables we will bisect
variables we will bisect 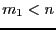 variables, which will lead to
variables, which will lead to
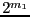 new boxes. This mode is obtained by setting
the global integer variable
ALIAS_Mixed_Bisection
to
new boxes. This mode is obtained by setting
the global integer variable
ALIAS_Mixed_Bisection
to 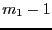 . Here we will order the variables according to the value of
their smear function (if the flag Single_Bisection is 2 or 3) or according to their width (for 1,4,5).
. Here we will order the variables according to the value of
their smear function (if the flag Single_Bisection is 2 or 3) or according to their width (for 1,4,5).




Next: Implementation
Up: Mathematical background
Previous: Improving the evaluation using
Contents
Jean-Pierre Merlet
2012-12-20
![]() variables we will bisect
variables we will bisect ![]() variables, which will lead to
variables, which will lead to
![]() new boxes. This mode is obtained by setting
the global integer variable
ALIAS_Mixed_Bisection
to
new boxes. This mode is obtained by setting
the global integer variable
ALIAS_Mixed_Bisection
to ![]() . Here we will order the variables according to the value of
their smear function (if the flag Single_Bisection is 2 or 3) or according to their width (for 1,4,5).
. Here we will order the variables according to the value of
their smear function (if the flag Single_Bisection is 2 or 3) or according to their width (for 1,4,5).