



Next: Implementation
Up: Rohn simplification procedure
Previous: Rohn simplification procedure
Contents
Let 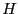 be the set of vector with components either -1 or 1 and
the scalar matrices
be the set of vector with components either -1 or 1 and
the scalar matrices 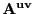 ,
,
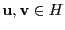 ,the set
of matrices
whose elements are
,the set
of matrices
whose elements are
The set of matrices 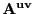 has
has 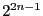 elements. If all
matrices in the set have a determinant of the same sign, then all the
matrices A are regular [22].
elements. If all
matrices in the set have a determinant of the same sign, then all the
matrices A are regular [22].
Note than another simplification procedure may be built by using the
spectral radius (see section 7.6).
Jean-Pierre Merlet
2012-12-20