



Next: Optimization
Up: Linear algebra
Previous: Characteristic polynomial
Contents
Spectral radius
Safe calculation of the spectral radius of a square real or interval
matrix may be obtained with the procedures
int Spectral_Radius(INTERVAL_MATRIX &AA,double eps,double *ro,int iter)
int Spectral_Radius(MATRIX &AA,double eps,double *ro,int inter)
where
- AA: the matrix
- eps: a real that will be used to increment the solutions
found for the median polynomial (i.e. the polynomial whose
coefficients are the mid-point of the interval coefficients of the
characteristic polynomial) until the polynomial evaluation does not
contain 0
- ro: the upper bound of the spectral radius
- iter: the maximal number of allowed iteration
These procedures return 1 on success, 0 on failure (in which case
increasing eps may be a good option) and -1 if the matrix is not
square.
The procedures
int Spectral_Radius(INTERVAL_MATRIX &AA,double eps,double *ro)
int Spectral_Radius(MATRIX &AA,double eps,double *ro)
may also be used with a maximum number of iteration fixed to 100.
If it intended just to show that the spectral radius is larger than a
given value seuil then you may use
int Spectral_Radius(INTERVAL_MATRIX &A,double eps,double *ro,double seuil);
int Spectral_Radius(MATRIX &A,double eps,double *ro,double seuil);
int Spectral_Radius(INTERVAL_MATRIX &A,double eps,double *ro,int iter,double seuil);
int Spectral_Radius(MATRIX &A,double eps,double *ro,int iter,double seuil);
Note that the calculation of the spectral radius may be used to check
the regularity of an interval matrix. Indeed let 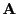 be an
interval matrix of dimension
be an
interval matrix of dimension  ,
, 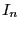 the identity matrix of
dimension
the identity matrix of
dimension  . If
. If 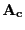 is the mid-matrix of
is the mid-matrix of 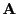 we may write
we may write
Let 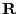 be an arbitrary matrix. It can be shown that if
be an arbitrary matrix. It can be shown that if
where 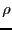 denotes the spectral radius, then
denotes the spectral radius, then 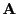 is
regular [22]: this is known as the Beeck-Ris test.
is
regular [22]: this is known as the Beeck-Ris test.




Next: Optimization
Up: Linear algebra
Previous: Characteristic polynomial
Contents
Jean-Pierre Merlet
2012-12-20