



Next: Solutions of differential and
Up: User's Guide
Previous: Univariate polynomials and series
Contents
Index
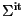 provides several types for computing with univariate
skew-polynomials or specific linear operators.
The most general is UnivariateSkewPolynomial,
for which you provide the Automorphism
provides several types for computing with univariate
skew-polynomials or specific linear operators.
The most general is UnivariateSkewPolynomial,
for which you provide the Automorphism 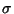 and the
and the 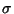 -derivation
-derivation 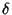 as parameters.
In addition, you also provide a usual polynomial type
that is meant to be used as internal representation for
the skew-polynomials. This lets you choose between dense
or sparse representation by selecting the appropriate
representation type. As for polynomials, naming the
variable is not necessary since the name is used only for output.
If you want to name the variable, pass a polynomial type with
a variable name as reprensentation type. There are several
ways to create the Automorphism
as parameters.
In addition, you also provide a usual polynomial type
that is meant to be used as internal representation for
the skew-polynomials. This lets you choose between dense
or sparse representation by selecting the appropriate
representation type. As for polynomials, naming the
variable is not necessary since the name is used only for output.
If you want to name the variable, pass a polynomial type with
a variable name as reprensentation type. There are several
ways to create the Automorphism 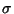 :
since Automorphism is of category Monoid,
the constant 1 can be used for the identity
map, while morphism is used for more
general maps.
:
since Automorphism is of category Monoid,
the constant 1 can be used for the identity
map, while morphism is used for more
general maps.
There are also types for common linear operators:
All of the above are implemented using a dense representation,
and allow an optional Symbol as last parameter if you
want to name the variable for output.
As for polynomials, when writing generic code for manipulating
skew-polynomials or operators, use a type parameter with the
appropriate category selected from Figure 2.




Next: Solutions of differential and
Up: User's Guide
Previous: Univariate polynomials and series
Contents
Index
Manuel Bronstein
2000-12-13