Usage
eigenring L
eigenring A
| Parameter | Type | Description |
|---|---|---|
| L |
|
A differential operator |
| A |
|
A matrix of fractions |
Description
eigenring(L) returns a basisof the eigenring of L, i.e.the set of operators
of order strictly less than the order of L and such that
for some operator S.
eigenring(A) returns anby
matrix
such that
for a basis of the eigenring of
, i.e. the set of matrices
such that
.
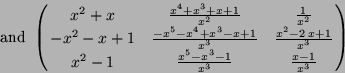
Example
We compute the eigenring of the differential system
as follows:
1 --> A := system(x^3,(x^5+x^2-3+x^4)/x^2,(-3+x^4+3*x)/x^2,
-x^3,-(x^5-3+x^4)/x^2,-(-x^2-3+x^4+3*x)/x^2,
x^3,(x^5-3+x^4)/x^2,(-3+x^4+3*x)/x^2);
2 --> e := eigenring(A);
3 --> tex(e);

This means that a basis of the eigenring of (3) is
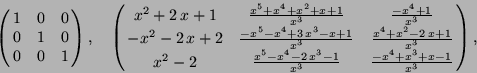
Usage within MAPLE
> A := matrix(3, 3, [x^3,(x^5+x^2-3+x^4)/x^2,(-3+x^4+3*x)/x^2,
-x^3,-(x^5-3+x^4)/x^2,-(-x^2-3+x^4+3*x)/x^2,
x^3,(x^5-3+x^4)/x^2,(-3+x^4+3*x)/x^2]);
> eigenring(A, D, x);
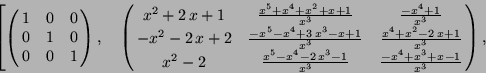
![\begin{displaymath}
\left.
\pmatrix{
x^{2}+x & {{x^{4}+x^{3}+x+1} \over {x^{2}}}...
...-x^{3}-1} \over {x^{3}}} & {{x-1} \over {x^{3}}}\cr }
\right]
\end{displaymath}](img99.png)