Experiment and traditional theory are essential components of the fusion energy science research program with a key overarching goal being to reach a level of scientific understanding to enable an accurate predictive capability of a burning tokamak plasma. Traditional theory makes simplifications to first-principles equations to enable analytical solutions in special limits. Simulation ideally bridges the gap of experiment and traditional theory by taking advantage of state-of-the-art development in applied mathematics, computer science, and high performance computers. However, the associated challenge of closing the gap between idealized (largely empirically-based) modeling and high-end first principles based simulations of mostly individual plasma dynamics is formidable. While the ideal goal is still far away, current progress has shortened the learning curve for developing more complete multiphysics models that are closer to the first-principles equations. Basically, the challenge involves capturing into more realistic reduced modules the most important physics trends produced by the aforementioned large scale first-principles codes that successfully simulate important individual phenomena in realistic 3D geometry. The most prominent and urgent scientific issues impacting the burning plasma program and the successful operation of the ITER experiment include: (1) disruption effects (large-scale macroscopic events producing rapid termination of plasma discharges), including avoidance and mitigation; (2) pedestal (steep-spatial gradient) formation and transient divertor heat loads in the plasma periphery; (3) Tritium migration and impurity transport; (4) performance optimization and scenario modeling; and (5) plasma feedback control. Each of the five questions is a computational grand challenge in its own right, and requires an integrated simulation capability. Of the five critical areas, the challenge of improved understanding of disruption effects, including avoidance and mitigation, is arguably the most important due to their potential to damage the actual plasma confinement device. When the plasma pressure exceeds linear MHD stability limits, a tokamak plasma is usually observed to disrupt. An important associated scientific challenge is to determine how close to such limits a disruption-free plasma discharge could be confidently expected to be sustainable.

|
ITER divertor geometry
CEA (French
Alternative Energies and Atomic Energy Commission) is active in four
main areas: low-carbon energies, defense and security, information
technologies and health technologies. In each of these fields, the
CEA maintains a cross-disciplinary culture of engineers and
researchers, building on the synergies between fundamental and
technological research.
IRFM
(Research Institute on Magnetic Fusion) develops a set of ab-initio
codes dedicated to magneto hydrodynamic (MHD) stability, turbulent
transport, plasma-wall interaction, and RF heating. This effort is
crucial to develop the expertise and skills in hot plasma physics as
well as in applied mathematics and computer science that are mandatory
to reach international recognition and play a role in the physics of
ITER when operating. Two non-linear MHD
codes are used. The first one, XTOR, is mainly dedicated to core
resistive MHD modes in connection with the scientific programme of
Tore Supra dedicated to long pulses, and of JET for Neoclassical
Tearing Modes (NTM). It is currently being coupled to a particle code
at CPhT (Ecole Polytechnique, Palaiseau, France) in order to study
kinetic MHD instabilities. The second code, JOREK, is rather
dedicated to Edge Localized Modes and disruptions. Regarding
transport, a full-F global gyrokinetic code, GYSELA, is being
developed. It can now operate with realistic geometry and soon with
several species. In addition, fluid codes are being developed to
compute core turbulence over times longer than the confinement times,
and also to model edge turbulence in both the scrape-off layer and
pedestal regions. Finally, 3 codes are being used for RF heating. The
EVE code is able to compute the propagation of RF waves in the IC
frequency range. LUKE is a Fokker-Planck code that computes the
distribution of fast electrons produced by LHCD and ECRH. It is
currently extended to compute the distribution of fast ions. Finally
MIKE is presently written in order to investigate the linear stability
of MHD modes driven by fast particles.
Significant recent progress in simulations of fine-scale turbulence
and in large-scale dynamics of magnetically confined plasmas has been
enabled by access to terascale supercomputers. These progress would
have been unreachable without innovative analytic and computational
methods for developing reduced descriptions of physics phenomena. In
particular, the plasma science community has developed advanced codes
for which computer runtime scales quite well with the number of
processors up to thousands cores. Accelerated progress on this
critical issue is especially important for ITER, because the size and
cost of a fusion reactor are determined by the balance between 1) loss
processes and 2) self-heating rates of the actual fusion reactions.
Realistic models, simulations and highly parallel algorithms are
essential in dealing with such challenges because of the huge range of
temporal and spatial scales involved. A good example of these
scalable tools is the GYSELA simulation software, developed at CEA
Cadarache. A realistic physics case has used 8192 processors during
one month to produce a 5D non-linear simulation. That kind of
simulation enhances scientific understanding of the nature of plasma
turbulence in fusion plasmas. Another example is the JOREK simulation
software. The main goal of JOREK is to allow for a significant
progress in understanding of largely unknown at present physics of
active control methods of plasma edge magnetoydrodynamic (so called
MHD) instabilities edge localized modes. They represent particular danger with
respect to heat and particle loads for Plasma Facing Components (PFC)
in ITER . The non-linear MHD theory can provide further physical and numerical improvements to refine knowledge of basic edge localized modes dynamics and related control techniques of these structures. In view of particular complexity of the problem the numerical simulations provide a key component of this effort, since computations are performed at a tiny fraction of the cost of a real experiment. To be effective, simulations are combined
with a well-focused, well-diagnosed experimental physics program to
guide model development, and to assure the validity of numerical
results.
GYSELA is a global non-linear electrostatic code which solves the
gyrokinetic equations (Vlasov) in a five dimensional phase space with
a semi-Lagrangian method. The purpose of the semi-Lagrangian method
is to take advantage of both the Lagrangian and Eulerian
approaches. In this approach the mesh grid is kept fixed in time in
the phase space (Eulerian method) and the Vlasov equation is
integrated along the trajectories (Lagrangian method) using the
invariance of the distribution function along the characteristics.
The 5D distribution function is updated thanks to this Vlasov
gyrokinetic equation. This equation is coupled with a Poisson-like
equation (named quasineutrality equation). The Poisson equation gives
the 3D electrostatic field generated by the distribution function of
the particles. The Semi-Lagrangian method is explicit and a
multilevel parallelism is accessible . The performed calculations with GYSELA
typically involve meshes with billions of grid points and thousands of
time steps. This code uses a scalable parallelization on today's
supercomputers combining distributed memory and shared memory programming.

|
Past time history of grand challenge plasma dynamics simulations with the GYSELA software
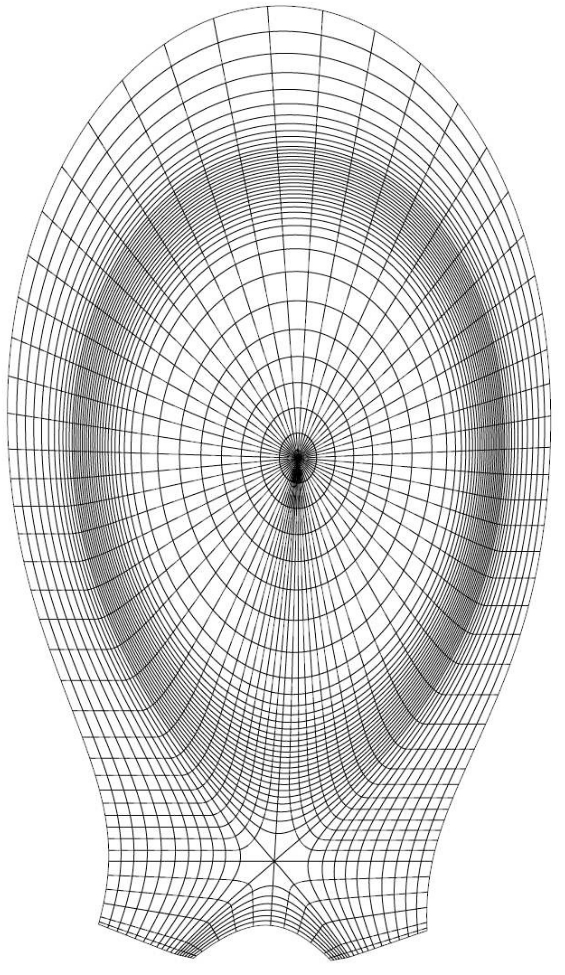
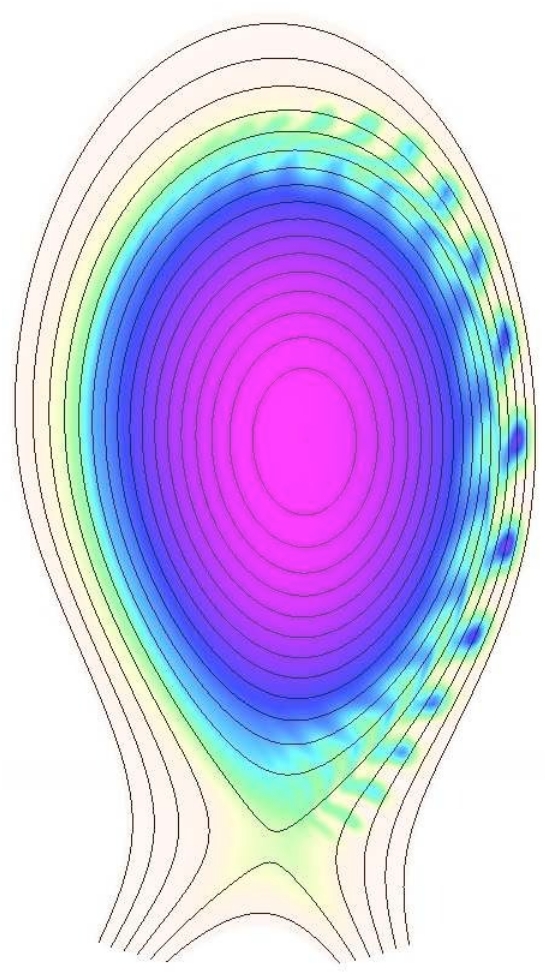
The JOREK code uses a fully implicit scheme for the time evolution of the MHD equations. This requires a solution of one large matrix containing all the degrees of freedom. This system of equations is solved using an external sparse solver. Mainly, JOREK makes use of direct methods for the sparse solver, using one of the following libraries: PasTiX or MUMPS. The limitation in the toroidal resolution is mostly due to the memory requirements of these direct methods. In order to reduce the memory requirements and possibly improve the scalability of the parallelization, iterative solvers have also been considered. A suitably preconditioned GMRES solver has been tried in JOREK, it works fine most of the time. The GMRES solver implemented in JOREK uses the submatrices of each toroidal harmonic as preconditioner. This solver allows for an increased toroidal resolution. But some limitations of JOREK remains: 1) no convergence of the GMRES solver for very non-linear physical feature, 2) high memory consumption of the sparse solver, 3) high spatial resolutions (larger than 200x300x32) are not achievable even with a large number of cores.
| 
|
MHD computation with the JOREK simulation software
